
 |
Новосибирский Государственный Технический Университет. |
МАШИННАЯ ГРАФИКА
(Учебное пособие в 3-х книгах)
Книга 2
П.В.Вельтмандер
Учебное пособие представляет собой семестровый курс лекций.
Содержит описание основных алгоритмов двух- трехмерной машинной
графики, включая алгоритмы реалистичного представления сцен.
Важную часть пособия составляют практические реализации алгоритмов на
языке С.
Как правило, приводится несколько реализаций для каждого алгоритма,
отличающихся различным выбором между наглядностью и эффективностью.
Курс ориентирован на две основные категории будущих специалистов:
Курс разбит на три части, выпущенные в виде отдельных книг:
ISBN ISBN 5-230-13606-5
© Новосибирский государственный университет, 1997
Данная, вторая часть курса лекций посвящена рассмотрению основных алгоритмов машинной графики.
В разделе 3 приводится алгоритм генерации окружностей.
В разделе 7 рассмотрены алгоритмы отсечения многоугольника.
В разделе 8 рассмотрены различные варианты организации данных.
В разделе 9 рассматривается геометрическое моделирование объектов и сцен.
Раздел 10 посвящен рассмотрению алгоритмов удаления скрытых линий и поверхностей.
В разделе 11 рассмотрены методы и алгоритмы реалистичного представления сцен.
Описание, конструирование, манипулирование и представление геометрических объектов являются центральными работами в графических системах. Их поддержка в требуемом объеме за счет соответствующих математических методов, алгоритмов и программ оказывают существенное влияние на возможности и эффективность графической системы. В данном разделе будут рассмотрены математические методы для описания геометрических преобразований координат в двух, трех и четырехмерном случае, будут обсуждены некоторые вопросы эффективности, рассмотрены геометрические преобразования растровых картин.
Далее большими буквами X, Y, Z будут обозначаться обычные декартовые координаты, а маленькие буквы x, y, z будут использоваться для обозначения т.н. однородных координат.
Преобразование сдвига в плоском случае имеет вид:
| (0.1.1) |
| (0.1.2) |
Преобразование масштабирования относительно начала координат имеет вид:
| (0.1.3) |
| (0.1.4) |
S = [
|
| ||
|
|
Преобразование поворота относительно начала координат имеет вид:
| (0.1.5) |
| (0.1.6) |
R = [
|
| ||
|
|
Столбцы и строки матрицы поворота представляют собой взаимно ортогональные единичные векторы. В самом деле квадраты длин векторов-строк равны единице:
|
|
|
Так как скалярное произведение векторов A ·B = |A| ·|B| ·cosy, где |A| - длина вектора A, |B| - длина вектора B, а y - наименьший положительный угол между ними, то из равенства 0 скалярного произведения двух векторов-строк длины 1 следует, что угол между ними равен 90°.
Аналогичное можно показать и для векторов-столбцов. Кроме того вектора-столбцы представляют собой такие единичные векторы, которые после выполнения преобразования, заданного этой матрицей, совпадут с осями. В самом деле, произведение первого столбца на матрицу есть
| (0.1.7) |
т.е. это единичный вектор вдоль оси X. Аналогично, произведение второго столбца на матрицу даст вектор [ 0 1 ]. Это позволяет сформировать матрицу, если известны результаты преобразования (см. пример в п. ).
Как видно из (2), (4) и (6) двумерные преобразования имеют различный вид. Сдвиг реализуется сложением, а масштабирование и поворот - умножением. Это различие затрудняет формирование суммарного преобразования и устраняется использованием двумерных однородных координат точки, имеющих вид:
|
Двумерные декартовые координаты точки получаются из однородных делением на множитель w:
| (0.1.8) |
Однородные координаты можно представить как промасштабированные с коэффициентом w значения двумерных координат, расположенные в плоскости с Z = w.
В силу произвольности значения w в однородных координатах не существует единственного представления точки, заданной в декартовых координатах.
Преобразования сдвига, масштабирования и поворота в однородных координатах относительно центра координат все имеют одинаковую форму произведения вектора исходных координат на матрицу преобразования.
Для сдвига
| (0.1.9) |
Для масштабирования
| (0.1.10) |
Для поворота
| (0.1.11) |
Как видно из (9) - (11), wn = w, а матрица преобразования для двумерных однородных координат в общем случае имеет вид:
| (0.1.12) |
Рассмотрим вначале для этого преобразование
|
Легко видеть, что xn = x, yn = y, h = S. Таким образом двумерные декартовые координаты преобразованной точки
|
Для уяснения смысла третьего столбца матрицы преобразований (12) выполним преобразование
|
| (0.1.13) |
Получим результирующие двумерные декартовые координаты Xn, Yn для преобразованной точки
|
| (0.1.14) |
|
|
Кроме удобств, связанных с единообразным представлением преобразований, и, следовательно, с упрощением композиции преобразований, рассматриваемой в следующем пункте, однородные координаты дают возможность простого представления точек, имеющих в декартовой системе значение координаты, равное бесконечности.
Рассмотрим в декартовой системе линию, проходящую через начало координат и точку (X,Y). Однородные координаты этой точки - (x,y,h) = (hX, hY, h), где h имеет произвольное значение. Предел отношения x/y при h стремящимся к 0 равен X/Y, но при этом декартовые координаты стремятся к бесконечности. Таким образом, точка с однородными координатами
| (0.1.15) |
Покажем, что прямые, параллельные в декартовой системе координат, в однородных координатах имеют точку пересечения. Эта особенность далее будет использована при анализе перспективных преобразований.
Пусть две пересекающиеся прямые в декартовой системе координат заданы системой уравнений:
| (0.1.16) |
Решая эту систему относительно X и Y, найдем координаты точки пересечения
|
|
Запишем результат в однородных координатах
|
В силу произвольности масштабного множителя, умножим значения координат на (A1 ·B2 - A2 ·B1)
|
|
При этом точка пересечения лежит на прямой -y0 ·x + x0 ·y = 0 на бесконечности.
Последовательное выполнение нескольких преобразований можно представить в виде единой матрицы суммарного преобразования. Умножение на единственную матрицу, естественно, выполняется быстрее, чем последовательное умножение на несколько матриц.
Рассмотрим сдвиг точки P0 на расстояние (Tx1, Ty1) в точку P1, а затем сдвинем точку P1 на расстояние (Tx2, Ty2) в точку P2. Обозначая через T1 и T2 матрицы сдвига, в соответствии с (9) получим:
|
|
|
Рассмотрим теперь последовательное выполнение масштабирований, первое с коэффициентами (Sx1, Sy1), второе с коэффициентами (Sx2, Sy2). Следует ожидать, что суммарное масштабирование будет мультипликативным. Обозначая через S1 и S2 матрицы масштабирования, в соответствии с (10) получим
|
|
Итак, получили, что результирующее масштабирование есть (Sx1 ·Sx2, Sy1 ·Sy2), т.е. суммарное масштабирование, вычисленное как произведение матриц, как и ожидалось, мультипликативно.
Аналогичным образом можно показать, что два последовательных поворота аддитивны.
Рассмотрим выполнение часто используемого поворота изображения на угол f относительно заданной точки P(X,Y). Это преобразование можно представить как перенос начала координат в точку (X,Y), поворот на угол f относительно начала координат и обратный перенос начала координат:
|
|
Суммарная матрица двумерных преобразований в однородных координатах имеет вид:
|
Вычисление преобразованных однородных координат точки P с непосредственным использованием T в выражении P ·T требует 9 операций умножения и 6 операций сложения. Но так как третья однородная координата может быть выбрана равной 1, а третий столбец T содержит единственный ненулевой элемент, равный 1, то преобразование декартовых координат может быть представлено в виде:
|
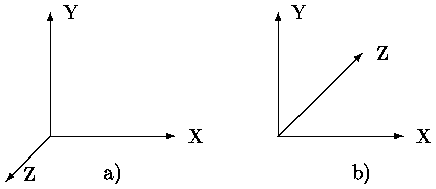
Далее при рассмотрении трехмерных преобразований, в основном, используется общепринятая в векторной алгебре правая система координат (рис. а). При этом, если смотреть со стороны положительной полуоси в центр координат, то поворот на +90° (против часовой стрелке) переводит одну положительную ось в другую (направление движения расположенного вдоль оси и поворачивающегося против часовой стрелки правого винта и положительной полуоси совпадают). В некоторых, специально оговариваемых случаях, используется левая система координат (см. рис. б). В левой системе координат положительными будут повороты по часовой стрелке, если смотреть с положительного конца полуоси. В трехмерной машинной графике более удобной является левая система координат. Тогда если, например, поверхность экрана совмещена с плоскостью XY, то большим удалениям от наблюдателя соответствую точки с большим значением Z (см. рис. б).
Работа с однородными трехмерными координатами и матрицами преобразования (формирование и композциция) подобна таковой для двумерного случая, поэтому здесь будут рассмотрены только матрицы преобразований сдвига, масштабирования и поворота и пример конструирования матрицы преобразования по известному его результату.
Подобно тому как в двумерном случае точка в однородных координатах представляется трехмерным вектором [ x y w ], а матрицы преобразований имеют размер 3×3, для трехмерного случая точка представляется четырехмерным вектором [ x y z w ], где w не равно 0, а матрицы преобразований имеют размер 4×4. Если w не равно 1, то декартовые координаты точки (X,Y,Z) получаются из соотношения:
|
|
|
В частности, матрица сдвига имеет вид:
|
Матрица масштабирования относительно центра координат имеет вид:
|
Ранее рассмотренная для двумерного случая матрица поворота (11) является в то же время трехмерным поворотом вокруг оси Z. Так как при трехмерном повороте вокруг оси Z (поворот в плоскости XY) размеры вдоль оси Z неизменны, то все элементы третьей строки и третьего столбца равны 0, кроме диагонального, равного 1:
|
При повороте вокруг оси X (в плоскости YZ) размеры вдоль оси X не меняются, поэтому все элементы первой строки и первого столбца равны 0, за исключением диагонального, равного 1:
|
При повороте вокруг оси Y (в плоскости XZ) размеры вдоль оси Y не меняются, поэтому все элементы второй строки и второго столбца равны 0, за исключением диагонального, равного 1:
|
Столбцы и строки подматриц 3×3 матриц поворота Rx, Ry, Rz, аналогично двумерному случаю, представляют собой взаимно ортогональные единичные векторы. Легко убедиться, что суммарная матрица преобразования для произвольной последовательности поворотов вокруг осей X, Y и Z имеет вид:
|
Взаимная ортогональность столбцов матрицы поворота и их совмещение с осями координат при преобразовании, задаваемом матрицей, позволяет легко сконструировать матрицу преобразования, если известны его результаты.
Пример формирования матрицы преобразования (из [])
Пусть заданы три точки P1, P2, P3. Найти матрицу преобразования такого, что после преобразования вектор P1P2 будет направлен вдоль оси Z, а вектор P1P3 будет лежать в плоскости YZ.
|
|
|
|
|
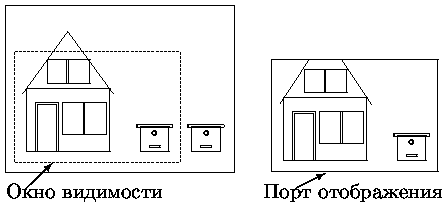
При визуализации двумерных изображений достаточно задать окно видимости в системе координат пользователя и порт отображения на экране дисплея, в котором будет выдаваться изображение из окна. В этом случае достаточно провести отсечение изображения по окну и выполнить двумерные преобразования окно-порт. На рис. показан простой пример двумерных преобразований. Окном отсекается часть изображения домика и один улей (см. рис. слева). Отсеченное изображение передается в порт отображения дисплея с выполнением преобразований окно-порт (см. рис. справа). В данном (простом) случае выполняется только преобразование сдвига.
В случае же трехмерных изображений отсечение выполняется уже не по окну, а по объему видимости и затем выполняется проецирование в порт отображения, который в свою очередь может быть проекцией объема видимости. Модель процесса визуализации трехмерных изображений приведена на рис. .

Как уже отмечалось, проецирование в общем случае - отображение точек, заданных в системе координат размерностью N, в точки в системе с меньшей размерностью. При отображении трехмерных изображений на дисплей три измерения отображаются в два.
Проецирование выполняется с помощью прямолинейных проекторов (проецирующих лучей), идущих из центра проекции через каждую точку объекта до пересечения с картинной поверхностью (поверхностью проекции). Далее рассматриваются только плоские проекции, при которых поверхность проекции - плоскость в трехмерном пространстве.
По расположению центра проекции относительно плоскости проекции различаются центральная и параллельные проекции.
При параллельной проекции центр проекции находится на бесконечном расстоянии от плоскости проекции. Проекторы представляют собой пучок параллельных лучей. В этом случае необходимо задавать направление проецирования и расположение плоскости проекции. По взаимному расположению проекторов, плоскости проекции и главных осей координат различаются ортогональные, прямоугольные аксонометрические и косоугольные аксонометрические проекции.
При ортогональной проекции проекторы перпендикулярны плоскости проекции, а плоскость проекции перпендикулярна главной оси. Т.е. проекторы параллельны главной оси.
При аксонометрической проекции имеется одна из двух перпендикулярностей:
Изображение, полученное при параллельном проецировании, не достаточно реалистично, но передаются точные форма и размеры, хотя и возможно различное укорачивание для различных осей.
При центральной проекции расстояние от центра проекции до плоскости проецирования конечно, поэтому проекторы представляют собой пучок лучей, исходящих из центра проекции. В этом случае надо задавать расположение и центра проекции и плоскости проекции. Изображения на плоскости проекции имеют т.н. перспективные искажения, когда размер видимого изображения зависит от взаимного расположения центра проекции, объекта и плоскости проекции. Из-за перспективных искажений изображения, полученные центральной проекцией, более реалистичны, но нельзя точно передать форму и размеры. Различаются одно, двух и трехточечные центральные проекции в зависимости от того по скольким осям выполняется перспективное искажение. Иллюстрация центральной проекции приведена на рис. .
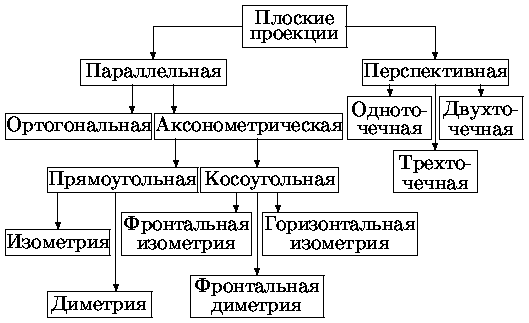
На рис. приведена классификация описанных выше плоских проекций.
Вначале мы рассмотрим ортогональные проекции, используемые в техническом черчении, в регламентированной для него правосторонней системе координат, когда ось Z изображается вертикальной. Затем будут проиллюстрированы аксонометрические проекции также в правосторонней системе координат, но уже более близкой к машинной графике (ось Y вертикальна, ось X направлена горизонтально вправо, а ось Z - от экрана к наблюдателю). Наконец выведем матрицы преобразования в левосторонней системе координат, часто используемой в машинной графике, с вертикальной осью Y, осью X, направленной вправо и осью Z, направленной от наблюдателя.
Использование проекций в техническом черчении регламентируется стандартом ГОСТ 2.317-69. Наиболее широко, особенно, в САПР используются ортогональные проекции (виды). Вид - ортогональная проекция обращенной к наблюдателю видимой части поверхности предмета, расположенного между наблюдателем и плоскостью чертежа.
В техническом черчении за основные плоскости проекций принимают шесть граней куба (рис. ).
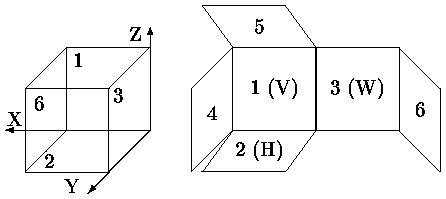
Очевидно, что при ортогональной проекции не происходит изменения ни углов, ни масштабов.
При аксонометрическом проецировании (см. рис. 0.4) сохраняется параллельность прямых, а углы изменяются; измерение же расстояний вдоль каждой из координатных осей в общем случае должно выполняться со своим масштабным коэффициентом.
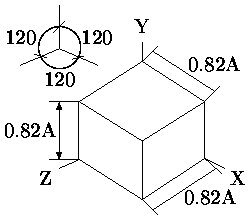
При изометрических проекциях укорачивания вдоль всех координатных осей одинаковы, поэтому можно производить измерения вдоль направлений осей с одним и тем же масштабом (отсюда и название изометрия). На рис. приведена (аксонометрическая прямоугольная) изометрическая проекция куба со стороной A. При этой проекции плоскость проецирования наклонена ко всем главным координатным осям под одинаковым углом. Стандартом регламентируется коэффициент сжатия, равный 0.82, а также расположение и взаимные углы главных координатных осей, равные 120° как это показано в левом верхнем углу рис. . Обычно сжатие не делается.
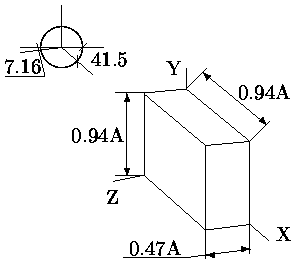
При диметрической проекции две из трех осей сокращены одинаково, т.е. из трех углов между нормалью к плоскости проекции и главными координатными осями два угла одинаковы. На рис. приведена (аксонометрическая прямоугольная) диметрическая проекция куба со стороной A. Там же показаны регламентируемые расположение осей и коэффициенты сжатия. Обычно вместо коэффициента сжатия 0.94 используется 1, а вместо 0.47 - 0.5.
В косоугольных проекциях плоскость проекции перпендикулярна главной координатной оси, а проекторы расположены под углом к ней. Таким образом, аксонометрические косоугольные проекции сочетают в себе свойства ортогональных и аксонометрических прямоугольных проекций.
Наиболее употребимы два вида косоугольной проекции - фронтальная (косоугольная) диметрия (проекция Kabinett - кабине) и горизонтальная (косоугольная) изометрия (проекция Kavalier - кавалье) или военная перспектива.
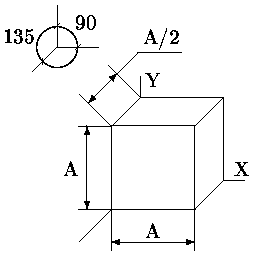
В случае фронтальной (косоугольной) диметрии при использовании правосторонней системы координат экрана плоскость проецирования перпендикулярна оси Z. Ось X направлена горизонтально вправо. Ось Z изображается по углом в 45° относительно горизонтального направления. Допускается угол наклона в 30 и 60°. При этом отрезки, перпендикулярные плоскости проекции, при проецирования сокращаются до 1/2 их истинной длины. На рис. приведена (аксонометрическая косоугольная) фронтальная диметрическая проекция куба со стороной A, там же показаны регламентируемые коэффициент сжатия, равный 0.5 и расположение осей.
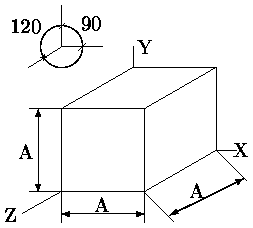
В случае же (аксонометрической косоугольной) горизонтальной изометрии, как следует из названия, плоскость проецирования перпендикулярна оси Y а укорачивания по всем осям одинаковы и равны 1. Угол поворота изображения оси X относительно горизонтального направления составляет 30°. Допускается 45 и 60° при сохранении угла 90° между изображениями осей X и Z. Иллюстрация этого приведена на рис. .
Выведем выражения для матриц преобразования, используя теперь левостороннюю систему координат более естественную для машинной графики.
Простейшее параллельное проецирование - ортогональное выполняется на плоскость, перпендикулярную какой-либо оси, т.е. при направлении проецирования вдоль этой оси. В частности, проецирование в XY-плоскость, заданную соотношением Z = Z0, выполняется следующим образом:
|
Рассмотрим теперь косоугольное проецирование, при котором плоскость проецирования перпендикулярна главной оси, а проекторы составляют с плоскостью проецирования угол не равный 90°. Матрица для этого преобразования может быть найдена исходя из значений угла проецирования и координат преобразованной точки. На рис. показана косоугольная параллельная проекция единичного куба.
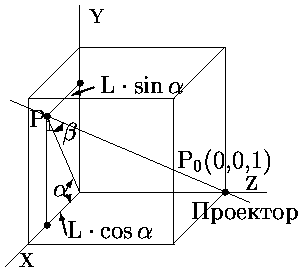
Из рисунка видно, что проектором, идущим из точки P0 в P1, точка P0(0,0,1) проецируется в P1(L·cosa, L·sina, 0).
Теперь проектором, параллельным рассмотренному (рис. ), спроецируем некоторую точку (X,Y,Z) в точку (Xp,Yp,Zp).
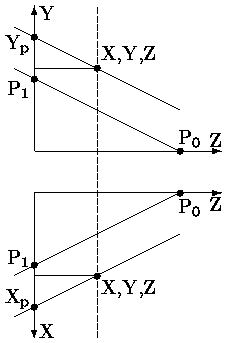
Из подобия треугольников получаем:
|
|
|
Различные варианты параллельных проекций формируются из полученной подстановкой значений L и углов a и b (см. рис. 0.10). В частности, для фронтальной косоугольной диметрии L = 1/2, следовательно, угол b между проекторами и плоскостью проецирования равен arctan2 = 63.4°. Угол же a, равен 45° и допускается 30 и 60°, как это сказано выше. (Обратите внимание, что в этой системе координат плоскость фронтальной проекции - плоскость XY, в отличие от системы координат технического черчения, где фронтальная проекция, как это показано на рис. 0.5, формируется в плоскости XZ).
Наиболее реалистично трехмерные объекты выглядят в центральной проекции из-за перспективных искажений сцены. Центральные проекции параллельных прямых, не параллельных плоскости проекции будут сходиться в точке схода. В зависимости от числа точек схода, т.е. от числа координатных осей, которые пересекает плоскость проекции, различаются одно, двух и трехточечные центральные проекции. Иллюстрация одно-, двух- и трехточечной центральных проекций куба приведена на рис. .
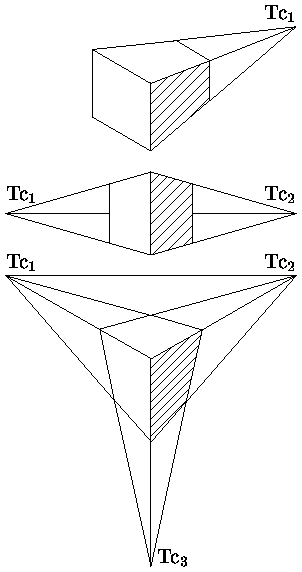
Наиболее широко используется двухточечная центральная проекция.
Выведем матрицу, определяющую центральное проецирование для простого случая одноточечной проекции (рис. ), когда плоскость проекции перпендикулярна оси Z и расположена на расстоянии d от начала координат. (Здесь используется удобная для машинной графики левосторонняя система координат).
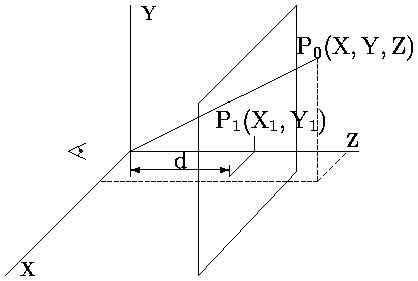
Начало отсчета находится в точке просмотра. Ясно, что изображения объектов, находящиеся между началом координат и плоскостью проекции увеличиваются, а изображения объектов, расположенных дальше от начала координат, чем плоскость проекции уменьшаются.
Из рис. 0.13 видно, что для координат (X1,Y1) точки P1, полученной проецированием точки P0(X,Y,Z) в плоскость Z = d (плоскость экрана) выполняются следующие соотношения:
|
|
|
Для перехода к декартовым координатам делим все на z/d и получаем:
|
|
|
|
Существенное повышение наглядности изображения достигается использованием псевдостереоизображений. В этом случае каждым глазом надо рассматривать отдельный перспективный вид. Оба таких вида отображаются на экран дисплея. Для их разделения могут использоваться:
· цветовое разделение, когда, например, изображение для левого глаза
строится красным цветом, а для правого - синим и для просмотра
используются цветные очки; недостаток этого способа состоит в том,
что по сути дела можно формировать только простые каркасные
изображения, но зато реализация проста и полностью используется
пространственное разрешение дисплея;
· пространственное-временное разделение, когда, например,
изображение для левого глаза строится в четных строках, а для
правого - в нечетных и для просмотра используются электронные или
электромеханические очки, перекрывающие или левый или правый глаз
на время прорисовки нечетных, четных строк, соответственно; этот
подход может быть реализован на дисплеях с чересстрочной
разверткой, позволяет выводить достаточно динамические цветные
полутоновые изображения, но с уменьшением вдвое разрешения по
вертикали;
· временное разделение, когда для левого глаза используется одна
страница видеопамяти, а для правого - вторая и происходит их
переключение с достаточно большой частотой кадровой развертки; для
перекрытия глаз также должны использоваться электронные или
электромеханические очки; пространственное разрешение по строкам
здесь не теряется.
Кроме этого, статические цветные псевдостереоизображения могут быть получены последовательным фотографированием изображений для левого и правого глаз с последующим просмотром через стереоскоп.
Используя результаты, полученные в предыдущем пункте, легко сконструировать матрицы преобразований для получения стереопроекций для левого и правого глаз.
Также как и для векторных изображений в двумерном случае, для растровых картин могут в общем случае требоваться преобразования сдвига, масштабирования и поворота. В связи с существенно дискретным характером изображения при выполнении этих преобразований имеется ряд особенностей.
Преобразование сдвига реализуется наиболее просто и заключается в переписывании части изображения (bitblt - операции Bit Block Transfer). При этом возможно исполнение некоторых операций над старым и новым пикселами с одинаковыми координатами.
Наиболее употребимыми являются:
· замена - новый пиксел просто заменяет старый,
· исключающее ИЛИ - в видеопамять заносится результат операции XOR
над старым и новым кодами пикселов. Эта операция обычно
используется дважды - вначале для занесения некоторого
изображения, например, перекрестия и повторного его занесения для
восстановления исходной картины.
Кроме этого, для реализации техники "акварель", т.е. техники работы с прозрачными цветами, в видеопамять заносится результат цветовой интерполяции между старым и новым оттенками пикселов. Эта операция всегда точно реализуема в полноцветных дисплеях, хранящих значения R, G и B в каждом пикселе. В дисплеях с таблицей цветности возможно получение не совсем правильных результатов.
Принято различать два типа масштабирования:
· целочисленное - zoom,
· произвольное, когда коэффициент масштабирования не обязательно целое число, - transfocation.
Наиболее просто реализуется целочисленное масштабирование. При увеличении в K раз каждый пиксел в строке дублируется К раз и полученная строка дублируется К раз. При уменьшении в K раз из каждой группы в K строк выбирается одна строка и в ней из каждой группы в K пикселов берется один пиксел в качестве результата. Не целочисленное масштабирование требует нерегулярного дублирования при увеличении и выбрасывания при уменьшении. Для отсутствия "дырок" в результирующем изображении при любых преобразованиях растровых картин следует для очередного пиксела результирующего изображения определить соответствующий (соответствующие) пикселы исходного изображения, вычислить значение пиксела и занести его.
Рассмотрим нецелочисленное уменьшение, т.е. перепись из большего массива в меньший (увеличение строится похожим образом).
Алгоритм ясен из следующей программы:
#define Max 13 // размер исходного массива
#define Min 7 // размер результирующего массива
int ist; // целая часть приращения индекса большего
// массива при смещении на 1 по меньшему
float rst; // дробная часть приращения индекса большего
// массива при смещении на 1 по меньшему
int iwr; // индекс записи
int ird; // целая часть индекса чтения
float rrd; // дробная часть индекса чтения
char isx[Max]; // исходный массив пикселов
char rez[Min]; // результирующий массив пикселов
void main (void) {
ist= (int)(Max / Min);
rst= (float)(Max - ist*Min)/(float)Min;
ird= 0; rrd= 0.0;
for (iwr=0; iwr < Min; iwr++) {
ird= ird + ist; // накопление целой части индекса;
rrd= rrd + rst; // накопление дробной части индекса;
if (rrd >= 1.0) {rrd= rrd - 1.0; ird= ird + 1; }
rez[iwr]= rez[ird-1];
}
}
Понятно, что такой алгоритм требует точной вещественной арифметики, версия алгоритма с целочисленной арифметикой имеет вид:
#define Max 13 // размер исходного массива
#define Min 7 // размер результирующего массива
int ist; // целая часть приращения индекса большего
// массива при смещении на 1 по меньшему
int rst; // остаток от приращения индекса
// меньшего массива
int iwr; // индекс записи
int ird; // целая часть индекса чтения
int rrd; // остаток индекса чтения
char isx[Max]; // исходный массив пикселов
char rez[Min]; // результирующий массив пикселов
void main (void) {
ist= (int)(Max / Min);
rst= Max - ist*Min;
ird= 0; rrd= 0.0;
for (iwr=0; iwr < Min; iwr++) {
ird= ird + ist; // накопление целой части индекса;
rrd= rrd + rst; // накопление дробной части индекса;
if (rrd >= Min) {rrd= rrd - Min; ird= ird + 1; }
rez[iwr]= rez[ird-1];
}
}
Внутренняя часть цикла при записи на ассемблере существенно упрощается, если использовать то, что для обычных 16-ти разрядных ЭВМ при переполнении происходит смена знака.
Определенные проблемы, связанные с дискретных характером изображения, возникают и при повороте растровой картины на угол не кратный 90°. Здесь возможны два подхода:
Назначение генератора векторов - соединение двух точек изображения отрезком прямой.
Далее будут рассмотрены четыре алгоритма:
· два алгоритма ЦДА - цифрового дифференциального анализатора
(DDA - Digital Differential Analyzer) для генерации векторов
- обычный и несимметричный;
· алгоритм Брезенхема для генерации векторов[];
· алгоритм Брезенхема для генерации ребер заполненного многоугольника с уменьшением ступенчатости.
Перед рассмотрением конкретных алгоритмов сформулируем общие требования к изображению отрезка:
· концы отрезка должны находиться в заданных точках;
· отрезки должны выглядеть прямыми,
· яркость вдоль отрезка должна быть постоянной и не зависеть от
длины и наклона.
Ни одно из этих условий не может быть точно выполнено на растровом дисплее в силу того, что изображение строится из пикселов конечных размеров, а именно:
· концы отрезка в общем случае располагаются на пикселах, лишь
наиболее близких к требуемым позициям и только в частных случаях
координаты концов отрезка точно совпадают с координатами
пикселов;
· отрезок аппроксимируется набором пикселов и лишь в частных случаях
вертикальных, горизонтальных и отрезков под 45° они будут
выглядеть прямыми, причем гладкими прямыми, без ступенек только
для вертикальных и горизонтальных отрезков
(рис. );
· яркость для различных отрезков и даже вдоль отрезка в общем случае различна, так как, например, расстояние между центрами пикселов для вертикального отрезка и отрезка под 45° различно (см. рис. ).

Объективное улучшение аппроксимации достигается увеличением разрешения дисплея, но в силу существенных технологических проблем разрешение для растровых систем приемлемой скорости разрешение составляет порядка 1280×1024.
Субъективное улучшение аппроксимации основано на психофизиологических особенностях зрения и, в частности, может достигаться просто уменьшением размеров экрана. Другие способы субъективного улучшения качества аппроксимации основаны на различных программных ухищрениях по "размыванию" резких границ изображения.
Далее в этом разделе рассмотрены три алгоритма генерации отрезка.
С помощью ЦДА решается дифференциальное уравнение отрезка, имеющее вид:
|
где Py = Yk - Yn - приращение координат отрезка по оси Y, а Px = Xk - Xn - приращение координат отрезка по оси X.
При этом ЦДА формирует дискретную аппроксимацию непрерывного решения этого дифференциального уравнения.
В обычном ЦДА, используемом, как правило, в векторных устройствах, тем или иным образом определяется количество узлов N, используемых для аппроксимации отрезка. Затем за N циклов вычисляются координаты очередных узлов:
|
|
Получаемые значения Xi, Yi преобразуются в целочисленные значения координаты очередного подсвечиваемого пиксела либо округлением, либо отбрасыванием дробной части.
Генератор векторов, использующий этот алгоритм, имеет тот недостаток, что точки могут прописываться дважды, что увеличивает время построения.
Кроме того из-за независимого вычисления обеих координат нет предпочтительных направлений и построенные отрезки кажутся не очень красивыми.
Аппаратная реализация этого алгоритма изложена в пункте 8.1 первой части курса.
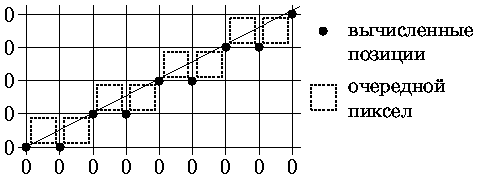
Субъективно лучше смотрятся вектора с единичным шагом по большей относительной координате (несимметричный ЦДА). Для Px > Py (при Px, Py > 0) это означает, что координата по X направлению должна увеличиться на 1 Px раз, а координата по Y-направлению должна также Px раз увеличиться, но на Py/Px.
Т.е. количество узлов аппроксимации берется равным числу пикселов вдоль наибольшего приращения.
Для генерации отрезка из точки (x1,y1) в точку (x2,y2) в первом октанте (Px і Py і 0) алгоритм несимметричного ЦДА имеет вид:
Пример генерации отрезка по алгоритму несимметричного ЦДА приведен на рис. .
В Приложении 2 приведена программа V_DDA, реализующая данный алгоритм.
Так как приращения координат, как правило, не являются целой степенью двойки, то в ЦДА-алгоритме (см. предыдущий пункт) требуется выполнение деления, что не всегда желательно, особенно при аппаратной реализации.
Брезенхем в работе [] предложил алгоритм, не требующий деления, как и в алгоритме несимметричного ЦДА, но обеспечивающий минимизацию отклонения сгенерированного образа от истинного отрезка, как в алгоритме обычного ЦДА. Основная идея алгоритма состоит в том, что если угловой коэффициент прямой < 1/2, то естественно точку, следующую за точкой (0,0), поставить в позицию (1,0) (рис. а), а если угловой коэффициент > 1/2, то - в позицию (1,1) (рис. б). Для принятия решения куда заносить очередной пиксел вводится величина отклонения Е точной позиции от середины между двумя возможными растровыми точками в направлении наименьшей относительной координаты. Знак Е используется как критерий для выбора ближайшей растровой точки.
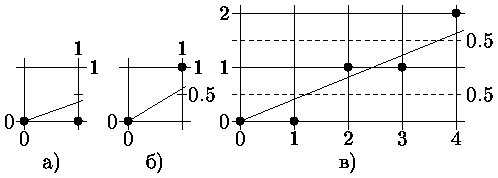
Если Е < 0, то точное Y-значение округляется до последнего меньшего целочисленного значения Y, т.е. Y-координата не меняется по сравнению с предыдущей точкой. В противном случае Y увеличивается на 1.
Для вычисления Е без ограничения общности упрощающе положим, что рассматриваемый вектор начинается в точке (0,0) и проходит через точку (4, 1.5) (см. рис. 0.3в), т.е. имеет положительный наклон меньший 1.
Из рис. 0.3в видно, отклонение для первого шага:
|
поэтому для занесения пиксела выбирается точка (1,0).
Отклонение для второго шага вычисляется добавлением приращения Y-координаты для следующей X-позиции (см. рис. 0.3в):
|
поэтому для занесения пиксела выбирается точка (2,1). Так как отклонение считается от Y-координаты, которая теперь увеличилась на 1, то из накопленного отклонения для вычисления последующих отклонений надо вычесть 1:
|
Отклонение для третьего шага:
|
поэтому для занесения пиксела выбирается точка (3,1).
Суммируя и обозначая большими буквами растровые точки, а маленькими - точки вектора, получаем:
|
Возможны случаи:
| Е1 > 0 | E1 Ј 0 |
| ближайшая точка есть: | |
| X1 = X0 + 1; Y1 = Y0 + 1; | X1 = X0 + 1; Y1 = Y0; |
| E2 = Е1 + Py/Px - 1; | E2 = E1 + Py/Px. |
Так как интересует только знак Е, то можно избавиться от неудобные частных умножением E на 2×Px:
| E1 = 2×Py - Px | |
| E1 > 0: | E2 = E1 + 2×(Py - Px) |
| E1 Ј 0: | E2 = E1 + 2×Py |
Таким образом получается алгоритм, в котором используются только целые
числа, сложение, вычитание и сдвиг:
X= x1;
Y= y1;
Px= x2 - x1;
Py= y2 - y1;
E= 2*Py - Px;
i= Px;
PutPixel(X, Y); /* Первая точка вектора */
while (i= i- 1 і 0) {
if (E і 0) {
X= X + 1;
Y= Y + 1;
E= E + 2*(Py - Px);
} else
X= X + 1;
E= E + 2*Py;
PutPixel(X, Y); /* Очередная точка вектора */
}
Этот алгоритм пригоден для случая 0 Ј dY Ј dX. Для других случаев алгоритм строится аналогичным образом.
На рис. приведен пример генерации по алгоритму Брезенхема того же самого отрезка, что и показанного на рис. 0.2 для генерации по алгоритму несимметричного ЦДА. Из сравнения рисунков видно, что результаты различны.
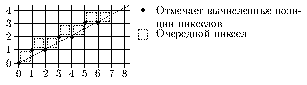
В Приложении 2 приведена программа V_BRE, реализующая описанный выше алгоритм.
Разработаны алгоритмы цифрового генератора для окружностей и других конических сечений.
Выше было отмечено, что растровая генерация отрезков имеет следующие
недостатки:
· неточное расположение начала и конца,
· ступенчатый вид отрезка,
· яркость зависит от наклона и длины.
Ясно, что первый недостаток не может быть устранен программным путем. Неравномерность яркости обычно не слишком заметна и может быть скомпенсирована очевидным образом, требующим, в общем случае, вещественной арифметики, но в связи с реально небольшим количеством различимых уровней яркости достаточно обойтись целочисленным приближением, причем очень грубым.
Наиболее заметно ухудшает качество изображения ступенчатость. Имеется следующие способы борьбы со ступенчатостью :
· увеличение пространственного разрешения за счет усовершенствования
аппаратуры,
· трактовка пиксела не как точки, а как площадки конечного размера,
яркость которой зависит от размера площади пиксела, занятой
изображением отрезка,
· "размывание" резкой границы, за счет частичной подсветки
пикселов, примыкающих к формируемому отрезку. Понятно, что при
этом ухудшается пространственное разрешение изображения.
В данном пункте мы рассмотрим модифицированный алгоритм Брезенхема, трактующий пиксел как конечную площадку. В следующем пункте будет рассмотрен общий подход, использующий низкочастотную фильтрацию для "размывания" границ изображения.
Основная идея алгоритма состоит в том, чтобы для ребер многоугольника устанавливать яркость пиксела пропорционально площади пиксела, попавшей внутрь многоугольника.
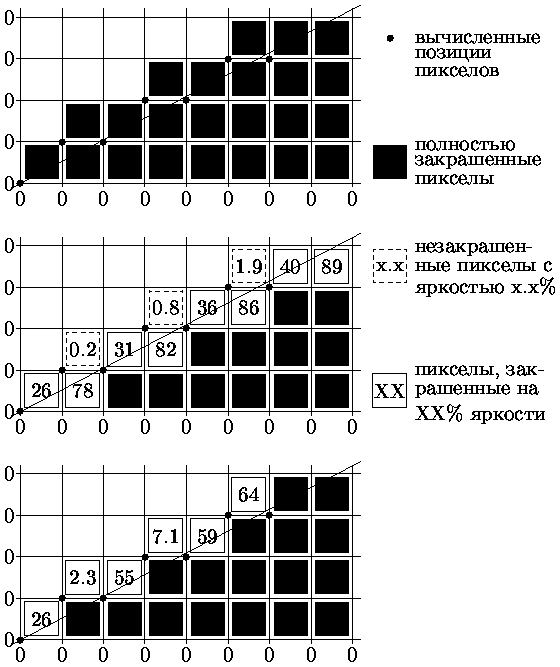
На рис. приведена иллюстрация построения ребра многоугольника с тангенсом угла наклона 11/21.
На рис. а) показан результат генерации многоугольника с использованием ранее рассмотренного алгоритма Брезенхема при двухуровневом изображении (пиксел или закрашен или не закрашен).
На рис. б) показан результат генерации многоугольника с вычислением интесивности пикселов, через которые проходит ребро многоугольника. Интенсивность вычисляется пропорциональной площади части пиксела, попавшей внутрь многоугольника.
На рис. в) показан результат генерации многоугольника с вычислением интесивности пиксела, через который проходит ребро многоугольника в соответствии с модифицированным алгоритмом Брезенхема.
Как видно из рис. при построении ребра многоугольника с тангенсом угла наклона t (0 Ј t Ј 1) могут захватываться либо один пиксел (пикселы (0,0), (2,1), (4,2), (6,8)) либо два пиксела (пикселы (1,0) и (1,1), (3,1) и (3,2), (5,2) и (5,3)). Если захватывается один пиксел, то часть его площади, попавшая внутрь многоугольника, равна dy + t/2 (рис. a).
Если же захватывается два пиксела, то часть площади нижнего пиксела, попавшая внутрь многоугольника равна 1 - [((1 - dy)2)/ 2t], а верхнего - [((dy - 1 + 2)2)/ 2t] (см. рис. б). Суммарная площадь частей для двух пикселов, попавшая внутрь многоугольника, равна dy + t/2.
Если теперь в исходном алгоритме Брезенхема (см. 0.2.2) заменить отклонение E на E' = E + (1-t), то 0 Ј E' Ј 1) и значение E' будет давать значение той части площади пиксела, которая находится внутри многоугольника.
Выполняя преобразование над значением отклонения для первого шага (см. 0.2.2) получим, что начальное значение станет равным 1/2. Максимальное значение отклонения E'max, при превышении которого производится увеличение Y-координаты занесения пикселов, станет равным (1 - t).
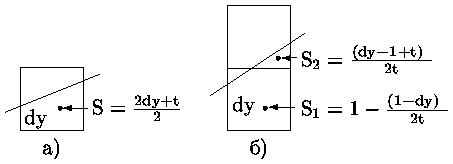
Для того, чтобы оперировать не дробной частью максимальной интенсивности, а непосредственно ее значениями достаточно домножить на полное число уровней интенсивности I тангенс угла наклона (t), начальное (E') и максимальное (E'max) значения отклонения.
В результате получается следующий алгоритм, пригодный для
случая 0 Ј dY Ј dX:
X= x1;
Y= y1;
Px= x2 - x1;
Py= y2 - y1;
t= I*Py / Px;
E'= I/2;
E'max= I - I*Py / Px;
i= Px;
PutPixel(X, Y, t/2); /* Первая точка вектора */
while (i = i - 1 і 0) {
if (E' і E'max) {
X= X + 1;
Y= Y + 1;
E' = E'- E'max;
} else
X= X + 1;
E' = E'+ t;
PutPixel(X, Y, E'); /* Очередная точка вектора */
}
Для избавления от вещественной арифметики при манипулировании с E' можно домножить уже упомянутые величины на 2*Px. Но в этом случае при занесении пикселов потребуется деление E' на 2*Px.
В Приложении 2 приведена процедура V_BreM, реализующая модифицированный алгоритм Брезенхема для генерации ребра заполненного многоугольника и пригодная для любого октанта.
Мы здесь рассмотрим методы, основанные на "размывании" границы.
Один из них заключается в том, что изображение строится с большим пространственным разрешением, чем позволяет дисплей. При выводе на экран атрибуты пиксела экрана вычисляются усреднением по группе пикселов изображения, построенного с большим разрешением. Т.е. пикселы изображения рассматриваются как подпикселы соответствующих пикселов экрана. Усредняющая маска перемещается по изображению с шагами, равными ее размеру.
Другой метод заключается в усреднении изображения без изменения его разрешения. В этом случае усредняющая маска перемещается по изображению с единичными шагами.
Очевидно, что первый метод должен давать более качественное изображение, но при больших затратах ресурсов. Для усреднения предложены различные маски ([,]).
Простейшее усреднение - равномерное (рис. ). Улучшить усреднение можно за счет использования весов, задающих влияние отдельных подпикселов на атрибут пиксела экрана (см. рис. ).
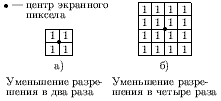
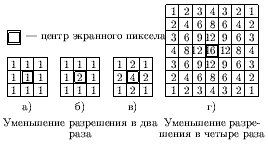
Эти массивы должны быть пронормированы для получения единичного коэффициента передачи, чтобы не вызывать неправильного смещения средней яркости изображения. Нормирующий коэффициент равен 1 / (сумму членов массива).
Ясно, что эти преобразования, примененные изображению зашумленному случайными импульсными помехами, будут подавлять шум. Это так называемые низкочастотные фильтры.
В Приложении 3 приведено несколько процедур фильтрации, реализующих оба рассмотренных метода - с понижением и без понижения разрешения.
Во многих областях приложений, таких как, например, системы автоматизированного проектирования машиностроительного направления, естественными графическими примитивами, кроме отрезков прямых и строк текстов, являются и конические сечения, т.е. окружности, эллипсы, параболы и гиперболы. Наиболее употребительным примитивом, естественно, является окружность. Один из наиболее простых и эффективных алгоритмов генерации окружности разработан Брезенхемом []. В переводной литературе он изложен, в частности, в [,].
Для простоты и без ограничения общности рассмотрим генерацию 1/8 окружности, центр которой лежит в начале координат. Остальные части окружности могут быть получены последовательными отражениями (использованием симметрии точек на окружности относительно центра и осей координат).
Окружность с центром в начале координат описывается уравнением:
|
Алгоритм Брезенхема пошагово генерирует очередные точки окружности, выбирая на каждом шаге для занесения пиксела точку растра Pi(Xi, Yi), ближайшую к истинной окружности, так чтобы ошибка:
|
была минимальной. Причем, как и в алгоритме Брезенхема для генерации отрезков, выбор ближайшей точки выполняется с помощью анализа значений управляющих переменных, для вычисления которых не требуется вещественной арифметики. Для выбора очередной точки достаточно проанализировать знаки.
Рассмотрим генерацию 1/8 окружности по часовой стрелке, начиная от точки X=0, Y=R.
Проанализируем возможные варианты занесения i+1-й точки, после занесения i-й.
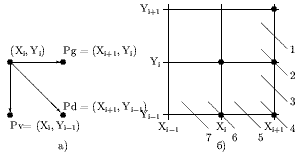
При генерации окружности по часовой стрелке после занесения точки (Xi, Yi) следующая точка может быть (см. рис. 0.1а) либо Pg = (Xi+1, Yi) - перемещение по горизонтали, либо Pd = (Xi+1, Yi-1) - перемещение по диагонали, либо Pv = (Xi, Yi-1) - перемещение по вертикали.
Для этих возможных точек вычислим и сравним абсолютные значения разностей квадратов расстояний от центра окружности до точки и окружности:
|
Выбирается и заносится та точка, для которой это значение минимально.
Выбор способа расчета определяется по значению Dd. Если Dd < 0, то диагональная точка внутри окружности. Это варианты 1-3 (см. рис. 0.1б). Если Dd > 0, то диагональная точка вне окружности. Это варианты 5-7. И, наконец, если Dd = 0, то диагональная точка лежит точно на окружности. Это вариант 4. Рассмотрим случаи различных значений Dd в только что приведенной последовательности.
Здесь в качестве следующего пиксела могут быть выбраны или горизонтальный - Pg или диагональный - Pd.
Для определения того, какой пиксел выбрать Pg или Pd составим разность:
|
И будем выбирать точку Pg при di Ј 0, в противном случае выберем Pd.
Рассмотрим вычисление di для разных вариантов.
Dg і 0 и Dd < 0, так как горизонтальный пиксел либо вне, либо на окружности, а диагональный внутри.
|
Добавив и вычтя (Y-1)2 получим:
|
В квадратных скобках стоит Dd, так что
|
Ясно, что должен быть выбран горизонтальный пиксел Pg. Проверка компонент di показывает, что Dg < 0 и Dd < 0, причем di < 0, так как диагональная точка больше удалена от окружности, т.е. по критерию di < 0 как и в предыдущих случаях следует выбрать горизонтальный пиксел Pg, что верно.
Здесь в качестве следующего пиксела могут быть выбраны или диагональный - Pd или вертикальный Pv.
Для определения того, какую пиксел выбрать Pd или Pv составим разность:
|
Если si Ј 0, то расстояние до вертикальной точки больше и надо выбирать диагональный пиксел Pd, если же si > 0, то выбираем вертикальный пиксел Pv.
Рассмотрим вычисление si для разных вариантов.
Dd > 0 и Dv Ј 0, так как диагональный пиксел вне, а вертикальный либо вне либо на окружности.
|
Добавив и вычтя (X+1)2 получим:
|
В квадратных скобках стоит Dd, так что
|
Ясно, что должен быть выбран вертикальный пиксел Pv. Проверка компонент si показывает, что Dd > 0 и Dv > 0, причем si > 0, так как диагональная точка больше удалена от окружности, т.е. по критерию si > 0 как и в предыдущих случаях следует выбрать вертикальный пиксел Pv, что соответствует выбору для вариантов 5 и 6.
Для компонент di имеем: Dg > 0 и Dd = 0, следовательно по критерию di > 0 выбираем диагональный пиксел.
С другой стороны, для компонент si имеем: Dd = 0 и Dv < 0, так что по критерию si Ј 0 также выбираем диагональный пиксел.
Итак:
Dd < 0
di Ј 0 - выбор горизонтального пиксела Pg
di > 0 - выбор диагонального пиксела Pd
Dd > 0
si Ј 0 - выбор диагонального пиксела Pd
si > 0 - выбор вертикального пиксела Pv
Dd = 0
выбор диагонального пиксела Pd.
Выведем рекуррентные соотношения для вычисления Dd для (i+1)-го шага,
после выполнения i-го.
1. Для горизонтального шага к Xi+1, Yi
Xi+1 = Xi + 1
Yi+1 = Yi
Ddi+1 = (Xi+1+1)2 + (Yi+1-1)2 - R2 =
Xi+12 + 2·Xi+1 + 1 + (Yi+1-1)2 - R2 =
(Xi+1)2 + (Yi-1)2 - R2 + 2·Xi+1 + 1 =
Ddi + 2·Xi+1 + 1
2. Для диагонального шага к Xi+1, Yi-1
Xi+1 = Xi + 1
Yi+1 = Yi - 1
Ddi+1 = Ddi + 2 ·Xi+1 - 2 ·Yi+1 + 2
3. Для вертикального шага к Xi, Yi-1
Xi+1 = Xi
Yi+1 = Yi - 1
Ddi+1 = Ddi - 2 ·Yi+1 + 1
В Приложении 5 приведена подпрограмма V_circle, реализующая описанный выше алгоритм и строящая дугу окружности в первой четверти. Начальная инициализация должна быть:
X= 0
Y= R
Dd = (X+1)2 + (Y-1)2 - R2 = 1 + (R-1)2 - R2 = 2*(1 - R)
Пикселы в остальных четвертях можно получить отражением. Кроме того достаточно сформировать дугу только во втором октанте, а остальные пикселы сформировать из соображений симметрии, например, с помощью подпрограммы Pixel_circle, приведенной в Приложении 5 и заносящей симметричные пикселы по часовой стрелке от исходного.
В Приложении 6 приведены подпрограмма V_BRcirc, реализующая описанный выше алгоритм и строящая дугу окружности во втором октанте с последующим симметричным занесением пикселов. Эта процедура может строить и 1/4 окружности. Подробнее см. текст Приложения 6. Там же приведена более короткая подпрограмма, строящая 1/8 окружности методом Мичнера [], (том 1, стр. 152). Остальная часть окружности строится симметрично.
В большинстве приложений используется одно из существенных достоинств растровых устройств - возможность заполнения областей экрана.
Существует две разновидности заполнения:
· первая, связанная как с интерактивной работой, так и с программным
синтезом изображения, служит для заполнения внутренней части
многоугольника, заданного координатами его вершин.
· вторая, связанная в первую очередь с интерактивной работой, служит
для заливки области, которая либо очерчена границей с кодом
пиксела, отличающимся от кодов любых пикселов внутри области, либо
закрашена пикселами с заданным кодом;
В данном разделе рассмотрим алгоритм заполнения многоугольника. В следующем разделе будут рассмотрены алгоритмы заливки области.
Простейший способ заполнения многоугольника, заданного координатами вершин, заключается в определении принадлежит ли текущий пиксел внутренней части многоугольника. Если принадлежит, то пиксел заносится.
Определить принадлежность пиксела многоугольнику можно, например, подсчетом суммарного угла с вершиной на пикселе при обходе контура многоугольника. Если пиксел внутри, то угол будет равен 360°, если вне - 0° (рис. ).
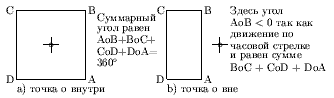
Вычисление принадлежности должно производиться для всех пикселов экрана и так как большинство пикселов скорее всего вне многоугольников, то данный способ слишком расточителен. Объем лишних вычислений в некоторых случаях можно сократить использованием прямоугольной оболочки - минимального прямоугольника, объемлющего интересующий объект, но все равно вычислений будет много. Другой метод определения принадлежности точки внутренней части многоугольника будет рассмотрен ниже при изучении отсечения отрезков по алгоритму Кируса-Бека.
Реально используются алгоритмы построчного заполнения, основанные на том, что соседние пикселы в строке скорее всего одинаковы и меняются только там где строка пересекается с ребром многоугольника. Это называется когерентностью растровых строк (строки сканирования Yi, Yi+1, Yi+2 на рис. ). При этом достаточно определить X-координаты пересечений строк сканирования с ребрами. Пары отсортированных точек пересечения задают интервалы заливки.
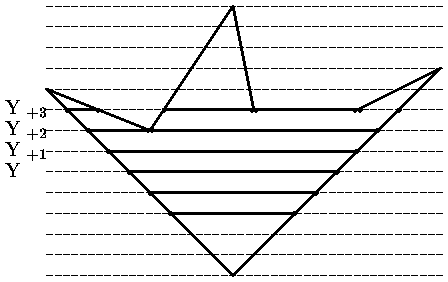
Кроме того, если какие-либо ребра пересекались i-й строкой, то они скорее всего будут пересекаться также и строкой i+1. (строки сканирования Yi и Yi+1 на рис. 0.2). Это называется когерентностью ребер. При переходе к новой строке легко вычислить новую X-координату точки пересечения ребра, используя X-координату старой точки пересечения и тангенс угла наклона ребра:
|
(тангенс угла наклона ребра - k = dy/dx, так как dy = 1, то 1/k = dx).
Смена же количества интервалов заливки происходит только тогда, когда в строке сканирования появляется вершина.
Учет когерентности строк и ребер позволяет построить для заполнения многоугольников различные высокоэффективные алгоритмы построчного сканирования. Для каждой строки сканирования рассматриваются только те ребра, которые пересекают строку. Они задаются списком активных ребер (САР). При переходе к следующей строке для пересекаемых ребер перевычисляются X-координаты пересечений. При появлении в строке сканирования вершин производится перестройка САР. Ребра, которые перестали пересекаться, удаляются из САР, а все новые ребра, пересекаемые строкой заносятся в него.
Общая схема алгоритма, динамически формирующего список активных ребер и заполняющего многоугольник снизу-вверх, следующая:
Если обнаруживаются горизонтальные ребра, то они просто
закрашиваются и информация о них в список активных ребер не
заносится.
Если после этого обнаруживается, что список активных ребер пуст,
то заполнение закончено.
В Приложении 5 приведены две подпрограммы заполнения многоугольника - V_FP0 и V_FP1. Первая реализует данный (простейший) алгоритм. Эта программа вполне работоспособна, но генерирует двух и трехкратное занесение части пикселов. Это мало приемлемо для устройств вывода типа матричных или струйных принтеров.
В отличие от V_FP0, в программе V_FP1 используется более сложный алгоритм формирования списка активных ребер, обеспечивающий практически полное отсутствие дублирований (рис. ).
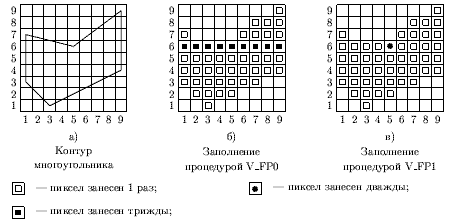
Понятно, что одна из важнейших работ в алгоритме построчного сканирования - сортировка. В связи с заведомо ограниченной разрешающей способностью растровых дисплеев (не более 2048) иногда целесообразно использовать чрезвычайно эффективный алгоритм сортировки методом распределяющего подсчета.
Для рассмотрения алгоритма предположим, что надо отсортировать числа, заданные в массиве с именем "Исходный_массив"; количество сортируемых чисел задается скаляром "Кол-во_чисел"; сортируемые числа J удовлетворяют условию:
|
Для сортировки потребуются описания:
int Max_число; /* Верхняя граница значений */ int *Повтор; /* Длина этого массива = Max_число */ int Кол_чисел; /* Кол-во сортируемых чисел */ int *Исходный_массив; /* Длина этого массива >= Кол_чисел */ int *Результат; /* Длина этого массива >= Кол_чисел */ int ii,jj, kk; /* Рабочие переменные */
for (ii=0; ii<Max_число; ++ii) Повтор[ii]= 0;
for (ii= 0; ii < Кол_чисел; ++ii) {
jj= Исходный_массив[ii];
Повтор[jj]= Повтор[jj] + 1;
}
jj= 0;
for (ii=0; ii<Max_число; ++ii) {
jj= jj + Повтор[ii];
Повтор[ii]= jj;
}
for (ii= 0; ii < Кол_чисел; ++ii) {
jj= Исходный_массив[ii];
kk= Повтор[jj];
Результат[kk]= jj;
Повтор[jj]= Повтор[jj] - 1;
}
Как уже отмечалось, для приложений, связанных в основном с интерактивной работой, используются алгоритмы заполнения области с затравкой.
При этом тем или иным образом задается заливаемая (перекрашиваемая) область, код пиксела, которым будет выполняться заливка и начальная точка в области, начиная с которой начнется заливка.
По способу задания области делятся на два типа:
· гранично-определенные, задаваемые своей (замкнутой) границей
такой, что коды пикселов границы отличны от кодов внутренней,
перекрашиваемой части области. На коды пикселы внутренней части
области налагаются два условия - они должны быть отличны от кода
пикселов границы и кода пиксела перекраски. Если внутри
гранично-определенной области имеется еще одна граница,
нарисованная пикселами с тем же кодом, что и внешняя граница, то
соответствующая часть области не должна
перекрашиваться;
· внутренне-определенные, нарисованные одним определенным кодом
пиксела. При заливке этот код заменяется на новый код
закраски.
В этом состоит основное отличие заливки области с затравкой от заполнения многоугольника. В последнем случае мы сразу имеем всю информацию о предельных размерах части экрана, занятой многоугольником. Поэтому определение принадлежности пиксела многоугольнику базируется на быстро работающих алгоритмах, использующих когерентность строк и ребер (см. предыдущий раздел). В алгоритмах же заливки области с затравкой нам вначале надо прочитать пиксел, затем определить принадлежит ли он области и если принадлежит, то перекрасить.
Заливаемая область или ее граница - некоторое связное множество пикселов. По способам доступа к соседним пикселам области делятся на 4-х и 8-ми связные. В 4-х связных областях доступ к соседним пикселам осуществляется по четырем направлениям - горизонтально влево и вправо и в вертикально вверх и вниз. В 8-ми связных областях к этим направлениям добавляются еще 4 диагональных. Используя связность мы может, двигаясь от точки затравки, достичь и закрасить все пикселы области.
Важно отметить, что для 4-х связной прямоугольной области граница 8-ми связна (рис. а) и наоборот у 8-ми связной области граница 4-х связна (см. рис. б). Поэтому заполнение 4-х связной области 8-ми связным алгоритмом может привести к "просачиванию" через границу и заливке пикселов в примыкающей области.
В общем, 4-х связную область мы можем заполнить как 4-х, так и 8-ми связным алгоритмом. Обратное же неверно. Так область на рис. а мы можем заполнить любым алгоритмом, а область на рис. б, состоящую из двух примыкающих 4-х связных областей можно заполнить только 8-ми связным алгоритмом.

С использованием связности областей и стека можно построить простые алгоритмы закраски как внутренне, так и гранично-определенной области. В [] рассматриваются совсем короткие рекурсивные подпрограммы заливки. В [] - несколько более длинные итеративные подпрограммы.
Рассмотрим простой алгоритм заливки гранично-определенной 4-х связной области. В [] приведена рекурсивная реализация подпрограммы заливки 4-х связной гранично-определенной области:
void V_FAB4R (grn_pix, new_pix, x_isx, y_isx)
int grn_pix, new_pix, x_isx, y_isx;
{
if (getpixel (x_isx, y_isx) № grn_pix &&
getpixel (x_isx, y_isx) № new_pix)
{
putpixel (x_isx, y_isx, new_pix);
V_FAB4R (grn_pix, new_pix, x_isx+1, y_isx);
V_FAB4R (grn_pix, new_pix, x_isx, y_isx+1);
V_FAB4R (grn_pix, new_pix, x_isx-1, y_isx);
V_FAB4R (grn_pix, new_pix, x_isx, y_isx-1);
}
} /* V_FAB4R */
Заливка выполняется следующим образом:
· определяется является ли пиксел граничным или уже закрашенным,
· если нет, то пиксел перекрашивается, затем проверяются и если надо перекрашиваются 4 соседних пиксела.
Полный текст тестовой программы V_FAB4R с использованием этой подпрограммы приведен в Приложении 6.
Понятно, что несмотря на простоту и изящество программы, рекурсивная реализация проигрывает итеративной в том, что требуется много памяти для упрятывания вложенных вызовов.
В [] приведен итеративный алгоритм закраски 4-х связной гранично-определенной области. Логика работы алгоритма следующая:
Поместить координаты затравки в стек
Пока стек не пуст
Извлечь координаты пиксела из стека.
Перекрасить пиксел.
Для всех четырех соседних пикселов проверить
является ли он граничным или уже перекрашен.
Если нет, то занести его координаты в стек.
На рис. а) показан выбранный порядок перебора соседних пикселов, а на рис. б) соответствующий ему порядок закраски простой гранично-определенной области.
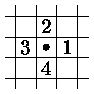
a) |
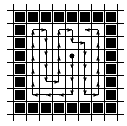
б) |
Ясно, что такой алгоритм экономнее, так как в стек надо упрятывать только координаты.
Рассмотренный алгоритм легко модифицировать для работы с 8-ми связными гранично-определенными областями или же для работы с внутренне-определенными.
Программа V_FAB4, реализующая данный алгоритм, приведена в Приложении 6.
Сравнительные прогоны тестовых программ V_FAB4R и V_FAB4 подтвердили соображения о неэкономности рекурсивного алгоритма: при стандартном окне стека в 64 K с помощью рекурсивной программы можно закрасить квадратик не более чем 57×57 пикселов. Итеративная же программа V_FAB4 при тех же условиях позволяет закрасить прямоугольник размером 110×110 истратив на массив координат 16382 байта.
Как уже отмечалось, очевидный недостаток алгоритмов непосредственно использующих связность закрашиваемой области - большие затраты памяти на стек, так как на каждый закрашенный пиксел в стеке по максимуму будет занесена информация о еще трех соседних. Кроме того, информация о некоторых пикселах может записываться в стек многократно. Это приведет не только к перерасходу памяти, но и потере быстродействия за счет многократной раскраски одного и того же пиксела. Значительно более экономен далее рассмотренный построчный алгоритм заливки.
Использует пространственную когерентность:
· пикселы в строке меняются только на границах;
· при перемещении к следующей строке размер заливаемой строки
скорее всего или неизменен или меняется на 1 пиксел.
Таким образом, на каждый закрашиваемый фрагмент строки в стеке хранятся координаты только одного начального пиксела [], что приводит к существенному уменьшению размера стека.
Последовательность работы алгоритма для гранично определенной области следующая:
В Приложении 6 приведена процедура V_FAST, реализующая рассмотренный алгоритм. За счет несложной модификации служебных процедур запроса и записи строк изображения, данная процедура может заливать изображение, размещенное в файле.
Если изображение выходит за пределы экрана, то на части дисплеев увеличивается время построения за счет того, что изображение строится в "уме". В некоторых дисплеях выход за пределы экрана приводит к искажению картины, так как координаты просто ограничиваются при достижении ими граничных значений, а не выполняется точный расчет координат пересечения (эффект "стягивания" изображения). Некоторые, в основном, простые дисплеи просто не допускают выхода за пределы экрана. Все это, особенно в связи с широким использованием технологии просмотра окнами, требует выполнения отсечения сцены по границам окна видимости.
В простых графических системах достаточно двумерного отсечения, в трехмерных пакетах используется трех и четырехмерное отсечение. Последнее выполняется в ранее рассмотренных однородных координатах, позволяющих единым образом выполнять аффинные и перспективные преобразования.
Программное исполнение отсечения достаточно медленный процесс, поэтому, естественно, в мощные дисплеи встраивается соответствующая аппаратура. Первое сообщение об аппаратуре отсечения, использующей алгоритм отсечения делением отрезка пополам и реализованной в устройстве Clipping Divider, появилось в 1968 г. [38]. Этот алгоритм был рассмотрен при изучении технических средств. Здесь мы рассмотрим программные реализации алгоритма отсечения.
Отсекаемые отрезки могут быть трех классов - целиком видимые, целиком невидимые и пересекающие окно. Очевидно, что целесообразно возможно более рано, без выполнения большого объема вычислений принять решение об видимости целиком или отбрасывании. По способу выбора простого решения об отбрасывании невидимого отрезка целиком или принятия его существует два основных типа алгоритмов отсечения - алгоритмы, использующие кодирование концов отрезка или всего отрезка и алгоритмы, использующие параметрическое представление отсекаемых отрезков и окна отсечения. Представители первого типа алгоритмов - алгоритм Коэна-Сазерленда (Cohen-Sutherland, CS-алгоритм) [4] и FC-алгоритм (Fast Clipping - алгоритм) [37]. Представители алгоритмов второго типа - алгоритм Кируса-Бека (Curus-Beck, CB - алгоритм) и более поздний алгоритм Лианга-Барски (Liang-Barsky, LB-алгоритм) [32].
Алгоритмы с кодированием применимы для прямоугольного окна, стороны которого параллельны осям координат, в то время как алгоритмы с параметрическим представлением применимы для произвольного окна.
Вначале мы рассмотрим алгоритм Коэна-Сазерленда, являющийся стандартом де-факто алгоритма отсечения линий и обладающий одним из лучших быстродействий при компактной реализации. Затем рассмотрим наиболее быстрый, но и чрезвычайно громоздкий FC-алгоритм. Далее рассмотрим алгоритм Лианга-Барски для отсечения прямоугольным окном с использованием параметрического представления. Быстродействие этого алгоритма сравнимо с быстродействием алгоритма Коэна-Сазерленда при большей компактности и наличии 3D и 4D реализаций. Последним рассмотрим алгоритм Кируса-Бека, который использует параметрическое представление и позволяет отсекать произвольным выпуклым окном. В заключение сравним быстродействие различных алгоритмов.
Этот алгоритм позволяет быстро выявить отрезки, которые могут быть или приняты или отброшены целиком. Вычисление пересечений требуется когда отрезок не попадает ни в один из этих классов. Этот алгоритм особенно эффективен в двух крайних случаях:
· большинство примитивов содержится целиком в большом окне,
· большинство примитивов лежит целиком вне относительно
маленького окна.
Идея алгоритма состоит в следующем:
Окно отсечения и прилегающие к нему части плоскости вместе образуют 9 областей (рис. 0.2.3). Каждой из областей присвоен 4-х разрядный код.
Две конечные точки отрезка получают 4-х разрядные коды, соответствующие областям, в которые они попали. Смысл разрядов кода:
1 рр = 1 - точка над верхним краем окна;
2 рр = 1 - точка под нижним краем окна;
3 рр = 1 - точка справа от правого края окна;
4 рр = 1 - точка слева от левого края окна.
Определение того лежит ли отрезок целиком внутри окна или целиком вне окна выполняется следующим образом:
· если коды обоих концов отрезка равны 0 то отрезок целиком
внутри окна, отсечение не нужно, отрезок принимается как
тривиально видимый (отрезок AB на рис. 0.2.3);
· если логическое & кодов обоих концов отрезка не равно нулю,
то отрезок целиком вне окна, отсечение не нужно, отрезок
отбрасывается как тривиально невидимый (отрезок KL на
рис. 0.2.3);
· если логическое & кодов обоих концов отрезка равно нулю, то
отрезок подозрительный, он может быть частично видимым (отрезки
CD, EF, GH) или целиком невидимым (отрезок IJ); для него нужно
определить координаты пересечений со сторонами окна и для каждой
полученной части определить тривиальную видимость или
невидимость. При этом для отрезков CD и IJ потребуется вычисление
одного пересечения, для остальных (EF и GH) - двух.
При расчете пересечения используется горизонтальность либо вертикальность сторон окна, что позволяет определить координату X или Y точки пересечения без вычислений.
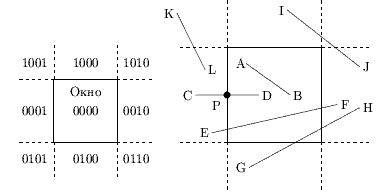
При непосредственном использовании описанного выше способа отбора целиком видимого или целиком невидимого отрезка после расчета пересечения потребовалось бы вычисление кода расположения точки пересечения. Для примера рассмотрим отрезок CD. Точка пересечения обозначена как P. В силу того, что граница окна считается принадлежащей окну, то можно просто принять только часть отрезка PD, попавшую в окно. Часть же отрезка CP, на самом деле оказавшаяся вне окна, потребует дальнейшего рассмотрения, так как логическое И кодов точек C и P даст 0, т.е. отрезок CP нельзя просто отбросить. Для решения этой проблемы Коэн и Сазерленд предложили заменять конечную точку с ненулевым кодом конца на точку, лежащую на стороне окна, либо на ее продолжении.
В целом схема алгоритма Коэна-Сазерленда следующая:
В цикле повторять пункты 2-6:
Эта схема реализована в процедуре V_CSclip, приведенной в Приложении 7.
В 1987 г. Собков, Поспишил и Янг [37] предложили алгоритм, названный ими FC-алгоритмом (Fast Clipping), также использующий кодирование, но не конечных точек, а линий целиком. Приведенное далее изложение алгоритма следует статье [37].
Схема кодирования близка к используемой в алгоритме Коэна-Сазерленда (рис. 0.2.4). Пространство разбивается на 9 неперекрывающихся областей, пронумерованных арабскими цифрами от 1 до 9. Коды, назначаемые концам отрезков, попавших в ту или иную область, приведены в двоичном и шестнадцатиричном виде (запись вида 0xD).
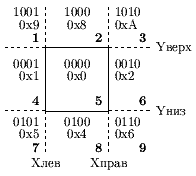
Отрезок видим только в области 5, т.е. отрезок, координаты которого удовлетворяют условиям:
|
Каждая конечная точка отрезка V0V1 окажется с одной из этих областей. Комбинация кодов концов отрезка, называемая кодом линии, используется для определения возможных вариантов расположения отрезка и, следовательно, отсечения. Код линии формируется из кодов концов отрезка следующим образом:
|
здесь Code(V1) обозначает код конечной точки V1,
Code(V0) × 16 означает сдвиг кода начальной
точки V0 влево на 4 разряда.
Так как каждый код может принимать одно из 9 значений, то всего имеется 81 возможный вариант расположения отрезка. Но, если Code(V0) равен Code(V1), то LineCode(V0,V1) равен LineCode(V1,V0). Имеется всего 9 таких случаев: 1-1, 2-2, ј 9-9. Следовательно, число различных случаев уменьшается до 72.
Каждый LineCode требует своего набора вычислений для определения отсечения отрезка за минимальное время. Всего имеется 8 основных случаев отсечения, а остальные симметричны к ним. Рассмотрим эти 8 основных случаев. При этом будут использоваться следующие обозначения:
· начальная точка отрезка считается точкой номер 0 (V0),
· конечная точка отрезка считается точкой номер 1 (V1),
· ClipA_B обозначает алгоритм расчета перемещения конечной
точки номер А на сторону окна B (расчет пересечения прямой
линии, на которой расположен отсекаемый отрезок со стороной
окна B).
Иллюстрации к случаям 1-7 приведены на рис. 0.2.5, для случая 8 - на рис. 0.2.6.
1. Начальная и конечная точки отрезка обе в области 5 (отрезок JK). Это простой случай принятия отрезка.
2. Начальная и конечная точки отрезка обе в области 4 (отрезок LA). Отрезок не пересекает видимую область, так что это простой случай отбрасывания.
3. Начальная точка в области 4, конечная - в области 1 (отрезок LB). Отрезок не пересекает видимую область, так что это простой случай отбрасывания.
4. Начальная точка в области 4, конечная - в области 2 (отрезки LC и LD). Отрезки явно пересекает Xлев, так что вначале надо определить соответствующую координату, используя алгоритм Clip0_Xleft. Для отрезка LC это дает V0y > Yверх, так что отрезок должен быть отброшен без дальнейших вычислений. Отрезок LD входит в окно с левой стороны и может выходить через верх. Следовательно, следующее отсечение должно быть Clip1_Top, после которого отрезок принимается.
5. Начальная точка в области 4, конечная - в области 3 (отрезки LE, LF и LG). Отрезки явно пересекает Xлев. Так же как и для случая 4 вначале применяется Clip0_Xleft и отрезок LE отбрасывается если V0y > Yверх. Если же получаем V0y Ј Yверх, то отрезок должен выйти из области видимости через верхнее или правое ребро. Применяем отсечение Clip1_Top и сравниваем новое значение X-координаты конечной точки - V1x c Xправ. Если V1x Ј Xправ, то отрезок (LF) проходит через верхнюю сторону, отрезок принимается и дальнейшие вычисления не нужны. Иначе отрезок (LG) проходит через правую сторону и требуется отсечение Clip1_Right. Отсечение закончено, отрезок принимается.
6. Начальная точка в области 4, конечная - в области 6 (отрезок LH). Данный отрезок видим. Вначале используем Clip0_Xleft затем Clip1_Right и принимаем отрезок.
7. Начальная точка в области 4, конечная - в области 5 (отрезок LI). Данный отрезок видим. Просто используем Clip0_Xleft и принимаем отрезок.
8. Начальная точка V0 (R, S, T или U) в области 7, конечная точка V1 (W, X, Y или Z) - в области 3 (см. рис.0.2.6). В этом случае могут быть отброшены только два типа отрезков. Для минимизации вычислений используем Clip0_Xleft. Если V0y > Yверх, то это первый случай отбрасывания (отрезок RW). Clip1_Xright и проверка V1y < Yниз задают второй случай отбрасывания (отрезок UZ). Все другие отрезки должны быть видимы. Если V0y < Yниз, тогда V0 = T, иначе V0 = S. Если V0y < Yниз, то Clip1_Ybottom даст точку V0 на ребре окна. Аналогично, если V1y > Yверх, то V1=X и здесь требуется Clip1_Ytop перед приемом отрезка. Если V1y < Yверх, тогда V1 = Y.
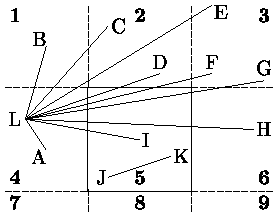
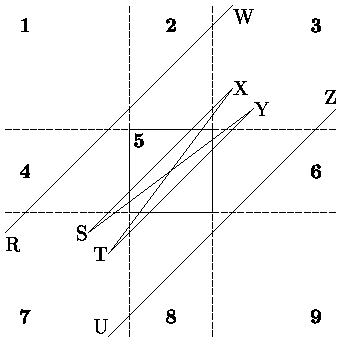
Из этих восьми случаев легко симметрично сгенерировать все остальные.
Главное отличие FC-алгоритма от алгоритма Коэна-Сазерленда состоит в упорядочивании действий по отсечению. Эффективность алгоритма Коэна-Сазерленда ограничивается последовательным характером и фиксированным порядком действий по отсечению. Как пример (см. рис. 0.2.6) отрезок RW будет отсекаться в порядке: сверху, снизу, справа и слева. Число же отсечений для определения видимости равно 2 - снизу и слева. В FC-алгоритме, напротив, для каждого значения LineCode имеется свой набор действий по отсечению. Для приведенного выше примера потребуется только одно отсечение для определения невидимости отрезка RW. Кроме этого, повышению эффективности FC-алгоритма по сравнению с CS-алгоритмом способствует отсутствие ненужных циклов и, следовательно, перевычислений кодов конечных точек.
В Приложении 7 приведена C-подпрограмма V_FCclip, реализующая FC-алгоритм и свободная от ошибок в подпрограмме, приведенной в [37]. Можно заметно сократить объем ее программного кода учтя симметрию и использовав указатели на данные либо переставляя данные. Например, в подпрограмме V_FCclip для отрезка LH (см. рис. 0.2.5, если он идет слева-направо вначале выполняется отсечение для начальной точки по левой стороне окна и затем для конечной - по правой. Если же отрезок идет справа-налево, то вначале вычисляется отсечение начальной точки по правой стороне и затем конечной - по левой. Очевидно, что эти два случая идентичны если поменять местами координаты начальной и конечной точек.
В 1982 г. Лианг и Барски [32] предложили алгоритмы отсечения прямоугольным окном с использованием параметрического представления для двух, трех и четырехмерного отсечения. По утверждению авторов, данный алгоритм в целом превосходит алгоритм Коэна-Сазерленда. Однако в работе [37] показывается, что это утверждение справедливо только для случая когда оба конца видимого отрезка вне окна и окно небольшое (до 50×50 при разрешении 1000×1000). Приведенное далее изложение двумерного варианта алгоритма следует, основном, работе [32].
Как уже говорилось, при 2D отсечении прямые отсекаются по 2D области, называемой окном отсечения. В частности, внутренняя часть окна отсечения может быть выражена с помощью следующих неравенств (рис. 0.2.7).
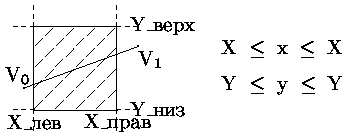
| (0.2.1) |
#tth_closerowВнутренняя часть окна отсечения
Продолжим каждую из четырех границ окна до бесконечных прямых. Каждая из таких прямых делит плоскость на 2 области. Назовем "видимой частью" ту, в которой находится окно отсечения, как это показано на рис. 0.2.8. Видимой части соответствует внутренняя сторона линии границы. Невидимой части плоскости соответствует внешняя сторона линии границы.
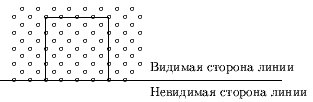
Таким образом, окно отсечения может быть определено как область, которая находится на внутренней стороне всех линий границ.
| (0.2.2) |
| (0.2.3) |
Или в общем виде для отрезка, заданного точками V0 и V1:
| (0.2.4) |
Для точек V0 и V1 параметр t равен 0 и 1, соответственно. Меняя t от 0 до 1 перемещаемся по отрезку V0V1 от точки V0 к точке V1. Изменяя t в интервале от -Ґ до +Ґ, получаем бесконечную (далее удлиненную) прямую, ориентация которой - от точки V0 к точке V1.
Однако вернемся к формальному рассмотрению алгоритма отсечения.
Подставляя параметрическое представление, заданное уравнениями (0.2.2) и (0.2.3), в неравенства (0.2.1), получим следующие соотношения для частей удлиненной линии, которая находится в окне отсечения:
| (0.2.5) |
Заметим, что соотношения (0.2.5) - неравенства, описывающие внутреннюю часть окна отсечения, в то время как равенства определяют его границы.
Рассматривая неравенства (0.2.5), видим, что они имеют одинаковую форму вида:
| (0.2.6) |
Здесь использованы следующие обозначения:
| (0.2.7) |
Вспоминая определения внутренней и внешней стороны линии границы (см. рис. 0.2.8), замечаем, что каждое из неравенств (0.2.6) соответствует одной из граничных линий (левой, правой, нижней и верхней, соответственно) и описывает ее видимую сторону. (Например, для i=1 имеем: P1·t Ј Q1 Ю -dx·t Ј x0 - XлевЮ x0 + dx·t і Xлев). Удлиним V0V1 в бесконечную прямую. Тогда каждое неравенство задает диапазон значений параметра t, для которых эта удлиненная линия находится на видимой стороне соответствующей линии границы. Более того, конкретное значение параметра t для точки пересечения есть t = Qi/Pi. Причем знак Qi показывает на какой стороне соответствующей линии границы находится точка V0. А именно, если Qi і 0, тогда V0 находится на видимой стороне линии границы, включая и ее. Если же Qi < 0, тогда V0 находится на невидимой стороне.
Рассмотрим Pi в соотношениях (0.2.7). Ясно, что любое Pi может быть меньше 0, больше 0 и равно 0.
Если Pi < 0, тогда соответствующее неравенство становится:
| (0.2.8) |
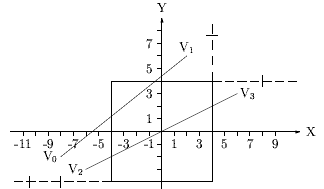
Для пояснения на рис. 0.2.10 показано пересечение с левой и правой границами при Pi < 0.
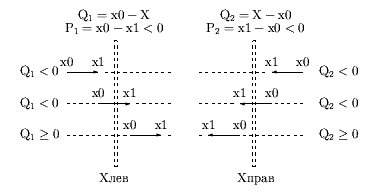
Очевидно, что диапазон значений параметра t, для которых удлиненная линия находится на видимой стороне соответствующей граничной линии, имеет минимум в точке пересечения направленной удлиненной линии, заданной вектором V0V1 и идущей с невидимой на видимую сторону граничной линии (так как только на границе t равно Qi / Pi, а в остальной части видимой стороны больше).
Аналогично, если Pi > 0, тогда соответствующее неравенство становится:
| (0.2.9) |
Для пояснения на рис. 0.2.11 показано пересечение с левой и правой границами при Pi > 0.
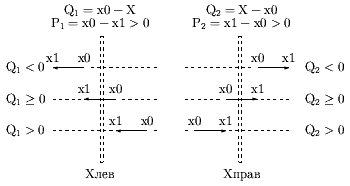
Так как значения параметра t только на границе равны Qi/Pi, а в остальной видимой части меньше Qi/Pi, то значение параметра t имеет максимум на границе.
Наконец, если Pi = 0, тогда соответствующее неравенство превращается в:
| (0.2.10) |
Заметим, что здесь нет зависимости от t, т.е. неравенство выполняется для всех t, если Qi і 0 и не имеет решения при Qi < 0. Для пояснения на рис. 0.2.12 иллюстрируется случай Pi = 0.
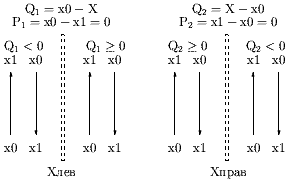
Геометрически, если Pi = 0, то нет точек пересечения
удлиненной линии, определяемой точками V0V1, с линиями границы.
Более того, если Qi < 0, то удлиненная линия находится на
внешней стороне линии границы, а при Qi і 0 находится на
внутренней стороне (включая ее). В последнем случае отрезок V0V1
может быть видим или нет в зависимости от того где находятся точки
V0V1 на удлиненной линии. В предыдущем же случае нет видимого
сегмента, так как удлиненная линия вне окна, т.е. это случай
тривиального отбрасывания.
Все эти случаи суммированы на блок-схеме, представленной на рис. 0.2.13.
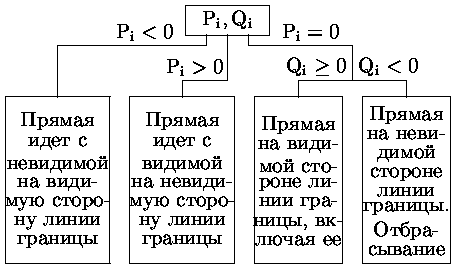
Итак, рассмотрение четырех неравенств дает диапазон значений параметра t, для которого удлиненная линия находится внутри окна отсечения. Однако, отрезок V0V1 только часть удлиненной линии и он описывается значениями параметра t в диапазоне: 0 Ј t Ј 1. Таким образом, решение задачи двумерного отсечения эквивалентно решению неравенств (0.2.6) при условии 0 Ј t Ј 1. Решение этой задачи сводится к далее описанному отысканию максимумов и минимумов.
Вспомним, что для всех i таких, что Pi < 0, условие видимости имеет вид: t і Qi / Pi. Из условия принадлежности точек удлиненной линии отрезку V0V1 имеем t і 0. Таким образом, нужно искать:
| (0.2.11) |
Аналогично, для всех i таких что Pi > 0, условие видимости - t Ј Qi / Pi и, следовательно, Ј 1.
| (0.2.12) |
Наконец, для всех i, таких что Pi = 0 следует проверить знак Qi. Если Qi < 0, то это случай тривиального отбрасывания, задача отсечения решена и дальнейшие вычисления не нужны. Если же Qi і 0, то информации, даваемой неравенством, недостаточно и это неравенство игнорируется.
Правая часть неравенств (0.2.11) и (0.2.12) - значения параметра t, соответствующие началу и концу видимого сегмента, соответственно. Обозначим эти значения как t0 и t1:
| (0.2.13) |
Если сегмент отрезка V0V1 видим, то ему соответствует интервал параметра:
| (0.2.14) |
Следовательно, необходимое условие видимости сегмента:
| (0.2.15) |
Но это недостаточное условие, так как оно игнорирует случай тривиального отбрасывания при Pi = 0, если Qi < 0. Тем не менее это достаточное условие для отбрасывания, т.е. если t0 > t1, то отрезок должен быть отброшен. Алгоритм проверяет, если Pi = 0 c Qi < 0, или t0 > t1 и в этом случае отрезок немедленно отбрасывается без дальнейших вычислений.
В алгоритме t0 и t1 инициализируются в 0 и 1, соответственно. Затем последовательно рассматривается каждое отношение Qi/Pi.
Если Pi < 0, то отношение вначале сравнивается с t1 и, если оно больше t1, то это случай отбрасывания. В противном случае оно сравнивается с t0 и, если оно больше, то t0 должно быть заменено на новое значение.
Если Pi > 0, то отношение вначале сравнивается с t0 и, если оно меньше t0, то это случай отбрасывания. В противном случае оно сравнивается с t1 и, если оно меньше, то t1 должно быть заменено на новое значение.
Наконец, если Pi = 0 и Qi < 0, то это случай отбрасывания.
На последнем этапе алгоритма, если отрезок еще не отброшен, то t0 и t1 используются для вычисления соответствующих точек. Однако, если t0 = 0, то конечная точка равна V0 и не требуется вычислений. Аналогично, если t1 = 1, то конечная точка - V1 и вычисления также не нужны.
Геометрический смысл этого процесса состоит в том, что отрезок удлиняется для определения где эта удлиненная линия пересекает каждую линию границы. Более детально, каждая конечная точка заданного отрезка V0V1 используется как начальное значение для конечных точек отсеченного отрезка C0C1. Затем вычисляются точки пересечения удлиненной линии с каждой линией границы (эти вычисления соответствуют вызову процедуры LB_tclip в программе). Если для данной линии границы направление, определяемое V0V1, идет с невидимой на видимую сторону линии границы, то эта точка пересечения вначале сравнивается с С1. Если точка находится далее вдоль линии, тогда C1 (и таким образом, С0С1) должна быть на невидимой стороне линии, поэтому отрезок должен быть отброшен. В противном случае точка пересечения сравнивается с С0; если точка далее вдоль линии, тогда С0 перемещается вперед к этой точке.
С другой стороны, если направление с видимой на невидимую сторону, тогда точка пересечения вначале сравнивается с С0. Если С0 далее вдоль линии, чем точка пересечения, тогда C0 (и, следовательно C0C1) находится на невидимой стороне линии границы, т.е. отрезок должен быть отброшен. В противном случае точка пересечения сравнивается с С1 и, если С1 далее вдоль линии, тогда С1 перемещается назад к точке пересечения.
Наконец, если удлиненная линия параллельна граничной линии и она на невидимой стороне, то отрезок отбрасывается. В конце алгоритма, если отрезок не отброшен, тогда C0 и С1 используются как конечные точки видимой части отрезка.
В Приложении 7 приведена C-подпрограмма V_LBclip, реализующая описанный выше алгоритм.
Все рассмотренные выше алгоритмы проводили отсечение по прямоугольному окну, стороны которого параллельны осям координат. Это, конечно, наиболее частый случай отсечения. Однако, во многих случаях требуется отсечение по произвольному многоугольнику, например, в алгоритмах удаления невидимых частей сцены. В этом случае наиболее удобно использование параметрического представления линий, не зависящего от выбора системы координат.
Из предыдущего пункта ясно, что для выполнения отсечения в параметрическом представлении необходимо иметь способ определения ориентации удлиненной линии, содержащей отсекаемый отрезок, относительно линии границы - с внешней стороны на внутреннюю или с внутренней на внешнюю, а также иметь способ определения расположения точки, принадлежащей отрезку, относительно окна - вне, на границе, внутри.
Для этих целей в алгоритме Кируса-Бека [29], реализующем отсечение произвольным выпуклым многоугольником, используется вектор внутренней нормали к ребру окна.
Внутренней нормалью Nв в точке А к стороне окна называется нормаль, направленная в сторону области, задаваемой окном отсечения.
Рассмотрим основные идеи алгоритма Кируса-Бека.
Так как многоугольник предполагается выпуклым, то может быть только две точки пересечения отрезка с окном. Поэтому надо найти два значения параметра t, соответствующие начальной и конечной точкам видимой части отрезка.
Пусть Ni - внутренняя нормаль к i-й граничной линии окна, а P = V1 - V0 - вектор, определяющий ориентацию отсекаемого отрезка, тогда ориентация отрезка относительно i-й стороны окна определяется знаком скалярного произведения Pi = Ni ·V, равного произведению длин векторов на косинус наименьшего угла, требуемого для поворота вектора Ni до совпадения по направлению с вектором V:
| (0.2.16) |
| (0.2.17) |
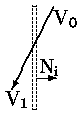
a) |
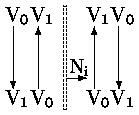
б) |
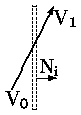
в) |
Для определения расположения точки относительно окна вспомним параметрическое представление отсекаемого отрезка:
| (0.2.18) |
Рассмотрим теперь скалярное произведение внутренней нормали Ni к i-й границе на вектор Q(t) = V(t) - Fi, начинающийся в начальной точке ребра окна и заканчивающийся в некоторой точке V(t) удлиненной линии.
| (0.2.19) |
Аналогично предыдущему имеем (рис. 0.2.15):
| (0.2.20) |
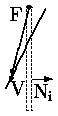
a) |
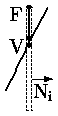
б) |
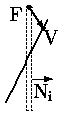
в) |
Подставляя в (0.2.19) параметрическое представление (0.2.18), получим условие пересечения отрезка с границей окна:
| (0.2.21) |
Раскрывая скобки, получим:
| (0.2.22) |
Используя (0.2.16) и (0.2.19) перепишем (0.2.21):
| (0.2.23) |
Разрешая (0.2.22) относительно t, получим:
| (0.2.24) |
Это уравнение и используется для вычисления значений параметров, соответствующих начальной и конечной точкам видимой части отрезка.
Как следует из (0.2.17), Pi равно нулю если отрезок либо вырожден в точку, либо параллелен границе. В этом случае следует проанализировать знак Qi и принять или не принять решение об отбрасывании отрезка целиком в соответствии с условиями (0.2.17).
Если же Pi не равно 0, то уравнение (0.2.24) используется для вычисления значений параметров t, соответствующих точкам пересечений удлиненной линии с линиями границ.
Алгоритм построен следующим образом:
Искомые значения параметров t0 и t1 точек пересечения инициализируются значениями 0 и 1, соответствующими началу и концу отсекаемого отрезка.
Затем в цикле для каждой i-й стороны окна отсечения вычисляются значения скалярных произведений, входящих в (0.2.23).
Если очередное Pi равно 0, то отсекаемый отрезок либо вырожден в точку, либо параллелен i-й стороне окна. При этом достаточно проанализировать знак Qi. Если Qi < 0, то отрезок вне окна и отсечение закончено иначе рассматривается следующая сторона окна.
Если же Pi не равно 0, то по (0.2.24) можно вычислить значение параметра t для точки пересечения отсекаемого отрезка с i-й границей. Так как отрезок V0V1 соответствует диапазону 0 Ј t Ј 1, то все решения, выходящие за данный диапазон следует отбросить. Выбор оставшихся решений определяется знаком Pi.
Если Pi < 0, т.е. удлиненная линия направлена с внутренней на внешнюю стороны граничной линии, то ищутся значения параметра для конечной точки видимой части отрезка. В этом случае определяется минимальное значение из всех получаемых решений. Оно даст значение параметра t1 для конечной точки отсеченного отрезка. Если текущее полученное значение t1 окажется меньше, чем t0, то отрезок отбрасывается, так как нарушено условие t0 Ј t1.
Если же Pi > 0, т.е. удлиненная линия направлена с внешней на внутреннюю стороны граничной линии, то ищутся значения параметра для начальной точки видимой части отрезка. В этом случае определяется максимальное значение из всех получаемых решений. Оно даст значение параметра t0 для начальной точки отсеченного отрезка. Если текущее полученное значение t0 окажется больше, чем t1, то отрезок отбрасывается, так как нарушено условие t0 Ј t1.
На заключительном этапе алгоритма значения t0 и t1 используются для вычисления координат точек пересечения отрезка с окном. При этом, если t0 = 0, то начальная точка осталась V0 и вычисления не нужны. Аналогично, если t1 = 1, то конечная точка осталась V1 и вычисления также не нужны.
Все эти случаи пояснены на блок-схеме, представленной на рис. 0.2.16.
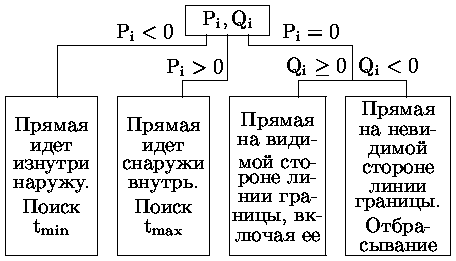
Вычисления значений параметров t0 и t1 выполняются в соответствии с выражениями (0.2.25).
| (0.2.25) |
В Приложении 7 приведена C-подпрограмма V_CBclip, реализующая описанный выше алгоритм.
Как видно из описания, алгоритм Кируса-Бека отсекает только по выпуклому окну. Кроме этого требуются значения внутренних нормалей к сторонам окна. Естественно выполнить эти вычисления в момент задания окна, так как следует ожидать, что одним окном будет отсекаться достаточно много отрезков.
Проверка на выпуклость может производиться анализом знаков векторных произведений смежных ребер (рис. 0.2.17).
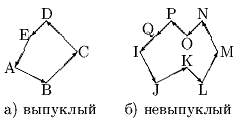
Если знак векторного произведения равен 0, то вершина вырождена, т.е. смежные ребра лежат на одной прямой (см. рис. 0.2.17 б), вершина Q).
Если все знаки равны 0, то многоугольник отсечения вырождается в отрезок.
Если же векторные произведения имеют разные знаки, то многоугольник отсечения невыпуклый (см. рис. 0.2.17 б)).
Если все знаки неотрицательные, то многоугольник выпуклый, причем обход вершин выполняется против часовой стрелки (см. рис. 0.2.17 а)), т.е. внутренние нормали ориентированы влево от контура. Следовательно вектор внутреннего перпендикуляра к стороне может быть получен поворотом ребра на +90° (в реализации алгоритма вычисления нормалей на самом деле вычисляется не нормаль к стороне, а перпендикуляр, так как при вычислении значения t по соотношению (0.2.22) длина не важна).
Если все знаки неположительные, то многоугольник выпуклый, причем обход вершин выполняется по часовой стрелке, т.е. внутренние нормали ориентированы вправо от контура. Следовательно вектор внутреннего перпендикуляра к стороне может быть получен поворотом ребра на -90°.
Описанный алгоритм реализован в процедуре V_SetPclip, приведенной в Приложении 7 и предназначенной для установки многоугольного окна отсечения.
Одновременное проведение операций проверки на выпуклость и разбиение простого невыпуклого многоугольника на выпуклые обеспечивается методом переноса и поворотов окна.
Алгоритм метода при обходе вершин многоугольника против часовой стрелки состоит в следующем:
Так как вновь полученные многоугольники могут в свою очередь оказаться невыпуклыми, алгоритм применяется к ним, пока все многоугольники не станут выпуклыми.
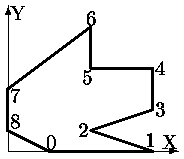
a) |
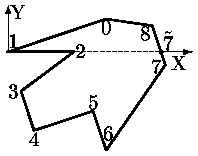
б) |
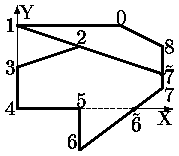
в) |
Повторное применение алгоритма в многоугольнику, образованному вершинами 2, 3, 4, 6, 7, [7\tilde], показано на рис. 0.2.18 в).
Данный алгоритм не обеспечивает минимальность числа вновь полученных выпуклых многоульников и некорректно работает если имеется самопересечение сторон, как это показано на рис. 0.2.19.
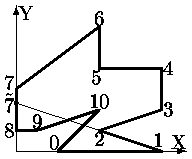
Во многих работах приводятся качественные соображения по быстродействию различных алгоритмов отсечения. В части работ, например, [32] или [37] приводятся результаты численных экспериментов по измерению скорости. Как правило, авторы работ этими экспериментами подтверждают преимущество своих алгоритмов.
В целом можно отметить несколько методических неточностей проведения таких экспериментов:
· неясно насколько одинаково хороши реализации собственного и
сравниваемых алгоритмов,
· эксперименты ([32] и [37] проводились в среде OC
UNIX и нет убедительных свидетельств отсутствия влияния окружения
на результаты,
· неясно насколько правильно выбиралось число повторений одного
отсечения относительно минимального измеряемого кванта
времени.
Исходя из этих соображений были проведены численные эксперименты по измерению быстродействия алгоритмов отсечения Коэна-Сазерленда, FC-алгоритма, Лианга-Барски и Кируса-Бека.
Использовались подпрограммы, приведенные в Приложении 7 при отсечении окнами различных размеров при полном разрешении
1000×1000. Процедуры транслировались и исполнялись на 486/DX4/100 в среде на Turbo C под управлением MS DOS 6.22.
Аналогично [37] были подготовлены 5 наборов данных по 1000 отрезков каждый со случайной генерацией конечных точек при следующих ограничениях:
1. Обе конечные точки отрезка внутри окна.
2. Одна конечная точка отрезка в окне, другая вне.
3. Обе конечные точки вне окна но с видимым сегментом.
4. Обе конечные точки вне окна и отрезок невидим.
5. Обе конечные точки генерировались случайно без ограничений.
Сгенерированные данные сохранялись в файлах и считывались в оперативную память перед очередным прогоном теста. Процедуры отсечения использовали данные из оперативной памяти. Для исключения временных затрат, связанных с организацией циклов и запросом координат отрезков, предварительно прогонялся тест с использованием "пустой" процедуры отсечения. Отсечение каждого отрезка проводилось 1000 раз. Измерение времени проводилось перед началом цикла по координатам.
Результаты измерений приведены в таблицах 0.2.3, 0.2.4, 0.2.5, 0.2.6, 0.2.7. Первая колонка таблиц - мои измерения. Вторая колонка таблиц - данные из [37]. Последние проводились на DEC VAX 8600 с ускорителем плавающей арифметики, транслировались C-компилятором без оптимизации и исполнялись под управлением ULTRIX V 1.1 (C).
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Многоугольники особенно важны в растровой графике как средство задания поверхностей.
Будем называть многоугольник, используемый в качестве окна отсечения, отсекателем, а многоугольник, который отсекается, - отсекаемым.
Алгоритм отсечения многоугольника должен в результате отсечения давать один или несколько замкнутых многоугольников (рис. 0.3.20). При этом могут быть добавлены новые ребра, а имеющиеся или сохранены или разделены или даже отброшены. Существенно, чтобы границы окна, которые не ограничивают видимую часть отсекаемого многоугольника, не входили в состав результата отсечения. Если это не выполняется, то возможна излишняя закраска границ окна (см. рис. 0.3.20б).
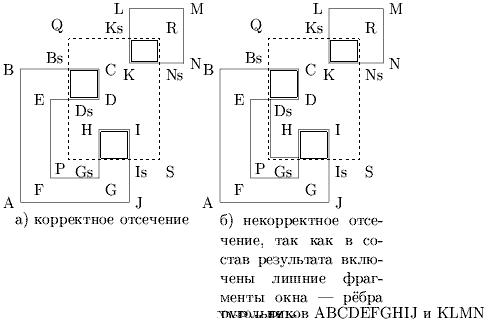
В принципе эту задачу можно решить с использованием рассмотренных выше алгоритмов отсечения линий, если рассматривать многоугольник просто как набор векторов, а не как сплошные закрашиваемые области. При этом вектора, составляющие многоугольник, просто последовательно отсекаются сторонами окна (рис. 0.3.21).
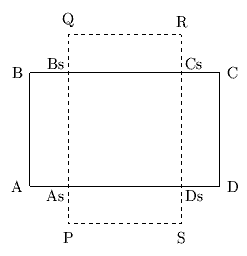
Если же в результате отсечения должен быть получен замкнутый многоугольник, то формируется вектор, соединяющий последнюю видимую точку с точкой пересечения с окном (рис. 0.3.22а). Проблема возникает при окружении отсекаемым многоугольником угла окна (см. рис. 0.3.22б).
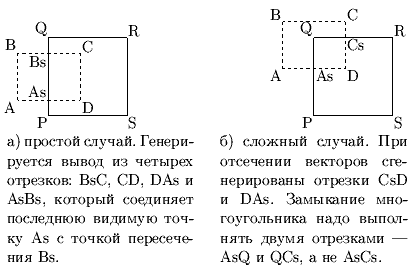
Здесь мы рассмотрим три алгоритма корректно решающие задачу отсечения сплошного многоугольника. Первые два алгоритма быстро работают, но генерируют лишние ребра, как это продемонстрировано на рис. 0.3.20б. Последний алгоритм свободен от указанного недостатка.
В общем, при отсечении многоугольников возникают два типа задач - отображение части изображения попавшей в окно и наоборот, отображение изображения, находящегося вне окна. Все здесь рассматриваемые алгоритмы могут использоваться в обоих случаях.
Простой метод решения проблемы охвата отсекаемым многоугольником вершины окна предлагается в алгоритме Сазерленда-Хогдмана [40], когда весь многоугольник последовательно отсекается каждой границей окна, как это показано на рис. 0.3.23.

При отсечении ребра, соединяющего очередную пару вершин K и L, возможны 4 случая взаимного расположения (рис. 0.3.24):
а) ребро на внутренней стороне границы,
б) ребро выходит из окна наружу,
в) ребро на внешней стороне границы,
г) ребро входит снаружи в окно.
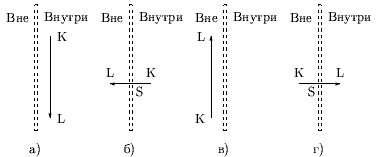
В случае а) в результат добавляется вершина L. В случае б) в результат заносится S - точка пересечения ребра с границей. В случае в) нет вывода. В случае г) выдаются точка пересечения S и конечная точка ребра L.
Для определения взаимного расположения и направленности используется векторное произведение вектора P1P2, проведенного из начальной в конечную точку текущего ребра окна, на вектор P1S из начальной точки текущего ребра окна в очередную вершину S многоугольника (рис. 0.3.25).
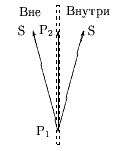
Предложена аппаратная реализация этого алгоритма, состоящая из четырех идентичных ступеней отсечения без промежуточной памяти [28].
В алгоритме Сазерленда-Ходгмана в результат могут заноситься границы окна, даже если они и не ограничивают видимую часть отсеченного многоугольника. Это можно устранить дополнительным анализом, либо используя более сложный алгоритм отсечения.
В данном разделе рассматривается простой алгоритм отсечения, который подобно алгоритму Сазерленда-Ходгмана может генерировать лишние стороны для отсеченного многоугольника, проходящие вдоль ребра окна отсечения. Но этот алгоритм несколько более быстрый и использует те же подпрограммы обработки многоугольного окна отсечения, что и алгоритм Кируса-Бека.
Многоугольник отсекается одним ребром выпуклого окна отсечения. В результате такого отсечения формируется новый многоугольник, который затем отсекается следующим ребром и т.д., пока не будет выполнено отсечение последним ребром окна.
Основная здесь процедура - процедура отсечения отдельным ребром, определяющая взаимное расположение очередной стороны многоугольника и ребра отсекателя и генерирующая соответствующие выходные данные.
Возможны 9 различных случаев расположения ребра окна и отсекаемой стороны, показанных на рис. 0.3.26-0.3.28.
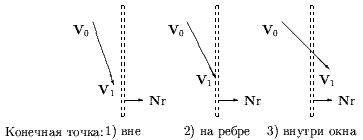
На них V0 и V1 - начальная и конечная точки отсекаемой стороны многоугольника, соответственно; Nr - нормаль к ребру окна отсечения, направленная внутрь окна.
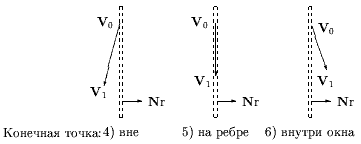
Из этих рисунков очевидны правила генерации выходных данных, зависящие от варианта взаимного расположения:
1) Нет выходных данных.
2) В выходные данные заносится конечная точка.
3) Рассчитывается пересечение и в выходные данные заносятся точка пересечения и конечная точка.
4) Нет выходных данных.
5) В выходные данные заносится конечная точка.
6) В выходные данные заносится конечная точка.
7) Рассчитывается пересечение и в выходные данные заносится только точка пересечения.
8) В выходные данные заносится конечная точка.
9) В выходные данные заносится конечная точка.
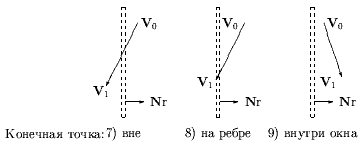
Для определения взаимного расположения, подобно алгоритму отсечения Кируса-Бека, используется скалярное произведение Q вектора нормали на вектор, проведенный из начала ребра в анализируемую точку. Пояснение см. на рис. 8.10.
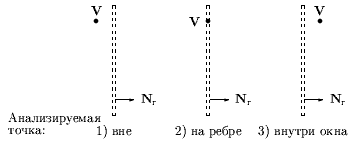
Таким образом, для определения взаимного расположения начальной V0 и конечной V1 точек отсекаемой стороны и ребра отсечения с вектором его начала R, надо вычислить:
|
|
Расчет пересечения, если он требуется, производится аналогично алгоритму Кируса-Бека с использованием параметрического представления линии:
|
Вначале находится значение параметра t для точки пересечения по формуле (см. описание алгоритма Кируса-Бека):
|
где Qn - скалярное произведение вектора нормали к ребру окна на вектор из начала ребра в начальную точку стороны, уже вычисленное при определении расположения начальной точки, а Pn = (V1 - V0)· Nr - скалярное произведение вектора нормали к ребру окна на вектор из начальной в конечную точки отсекаемой стороны.
Легко выразить это произведение через уже вычисленные величины Qn и Qk:
|
Таким образом, точке пересечения соответствует значение параметра t, равное:
|
Значения координат пересечения находятся из:
|
Описанный алгоритм реализован в процедуре V_Plclip, приведенной в Приложении 8.
В предыдущих разделах были рассмотрены два алгоритма отсечения многоугольника, последовательно отсекающие произвольный (как выпуклый, так и невыпуклый) многоугольник каждой из сторон выпуклого окна. Зачастую же требуется отсечение по невыпуклому окну. Кроме того оба рассмотренных алгоритма могут генерировать лишние стороны для отсеченного многоугольника, проходящие вдоль ребра окна отсечения. Далее рассматриваемый алгоритм Вейлера-Азертона [41,,] свободен от указанных недостатков ценой заметно большей сложности и меньшей скорости работы.
Предполагается, что каждый из многоугольников задан списком вершин, причем таким образом, что при движении по списку вершин в порядке их задания внутренняя область многоугольника находится справа от границы.
В случае пересечения границ и отсекаемого многоугольника и окна возникают точки двух типов:
· входные точки, когда ориентированное ребро отсекаемого
многоугольника входит в окно,
· выходные точки, когда ребро отсекаемого многоугольника идет с
внутренней на внешнюю стороны окна.
Общая схема алгоритма Вейлера-Азертона для определения части отсекаемого многоугольника, попавшей в окно, следующая:
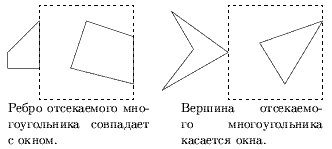
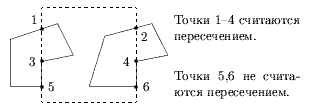
Модификация этого алгоритма для определения части отсекаемого многоугольника, находящейся вне окна, заключается в следующем:
· исходная точка пересечения пересечения берется из списка
выходных точек,
· движение по списку вершин окна выполняется в обратном порядке,
т.е. так чтобы внутренняя часть отсекателя была слева.
На рис. 0.3.31 иллюстрируется отсечение многоугольника ABCDEFGHI окном PQRS по алгоритму Вейлера-Азертона.
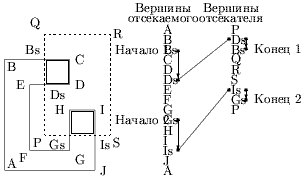
Начиная с этого алгоритма, при рассмотрении многих дальнейших требуется представления о различных структурах данных и работе с ними. Следующий раздел и посвящен беглому рассмотрению некоторых наиболее важных структур данных.
В данном разделе рассмотрены три основных способа работы с данными: последовательный доступ, непосредственный доступ, и списки. Данные могут быть организованы в виде:
· элементов данных (data item) - единичная информация, перерабатываемая системой,
· запись (record) - совокупность некоторого числа элементов данных,
· файл (file) - совокупность некоторого числа записей.
В общем случае структура данных образуется посредством упорядочивания записей и связей между ними в файл. В зависимости от требуемых операций данные в файле организуются различным образом.
Зачастую требуется простейшая последовательная обработка записей. Для этого достаточна последовательная организация данных, когда записи запоминаются в файле в последовательности поступления.
Выбор требуемой записи в файле с последовательной организацией возможен только путем его сканирования от начала до требуемой записи.
Удаление и/или вставка не последней записи приводят к большим перемещениям данных (рис. 0.4.32, 0.4.33).

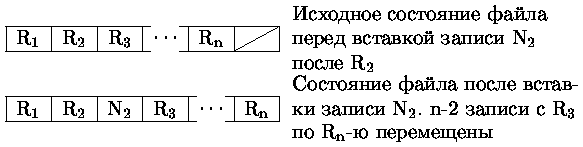
Частными, широко используемыми случаями последовательного доступа, являются очереди и стеки. Наиболее широко используются стеки.
Очередь - файл данных с дисциплиной обслуживания первым пришел - первым обслужен (FIFO - First Input First Output) (рис 0.4.34).
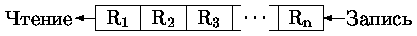
Стек (магазин, гнездовая память, память LIFO) - файл данных с дисциплиной обслуживания первым пришел - последним обслужен (LIFO - Last Input First Output).
Состояние стека определяется значением указателя стека, инициируемом при его создании. Для работы с созданным стеком достаточны две операции:
· PUSH - помещение записи в стек,
· POP - получение записи из стека.
Эти операции заносят/читают данные и модифицируют значение указателя стека. Стек может быть организован двумя способами, отличающимися правилами продвижения указателя стека:
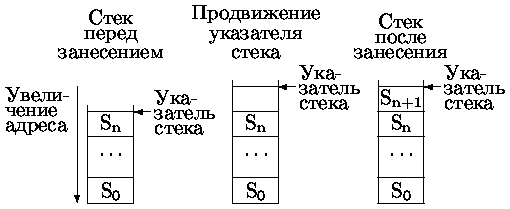
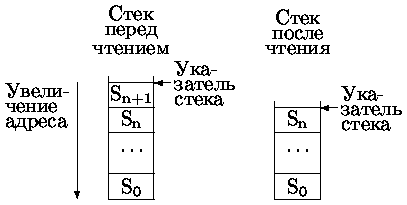
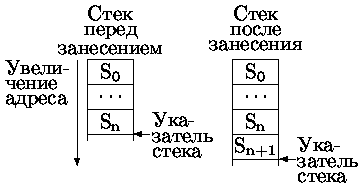
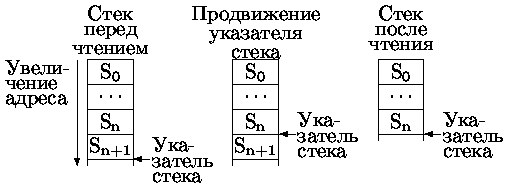
Наиболее часто используется первый способ организации стека.
При необходимости непосредственного доступа (random access) устанавливается связь между адресом запоминания и ключом, по которому ищется запись.
В простейшем случае ключ поиска - просто номер записи. Чаще ключ - некоторая совокупность данных из записи. По значению ключа либо непосредственно вычисляется адрес записи (например, адрес расположения физического блока фиксированной длины на диске вычисляется по его номеру), либо ключ используется для доступа к справочнику, в котором отыскивается адрес (например, адрес начала расположения i-го файла задается i-й записью в директории). Метод очень быстрый - мы немедленно получаем доступ к записи. Но он может быть очень расточительным по использованию памяти, когда из полного возможного набора в N ключей, по которым вырабатываются адреса в диапазоне от 0 до N-1, фактически будет иметься только K << N ключей, т.е. из всего диапазона адресов 0-(N-1) будет использоваться только K адресов, раскиданных по всему объему от 0 до N-1.
В таких случаях значение ключа используется для вычисления функции расстановки (hash code), определяющей адрес расположения данных. Причем функция расстановки подбирается такой, чтобы для K ключей из полного допустимого набора в N ключей, генерируемое количество адресов L было возможно более близко к K. Этот подход обычно используется при поиске информации об объекте по его имени, например, для поиска информации об объекте по его наименованию, для поиска информации в базе данных о сотруднике по его фамилии, для работы с таблицей идентификаторов в трансляторах и т.д. В этом случае функция расстановки вычисляется из символов ключа. Идеальная функция расстановки должна вычислять уникальный адрес для каждого из фактических ключей. Реальные же функции расстановки могут для разных ключей давать один и тот же адрес. Рассмотрим частный пример (табл. 9.1) занесения информации в таблицу из 10 элементов (L равно 10). В качестве ключа используем наименование объекта. Для вычисления хеш-адреса Hn в диапазоне 0-9 суммируем коды символов ключа, из которых предварительно вычитаем 65. В качестве хеш-адреса берем остаток от деления полученной суммы на 10. (На самом деле число 10 не годится, а выбрано для наглядности).
| Пример вычисления хеш-адреса. | Таблица 9.1 | |||||||
| Ключ | Коды символов ключа | Хеш-адрес | ||||||
| GALLERY | 71 | 65 | 76 | 76 | 69 | 82 | 89 | 3 |
| HOUSE | 72 | 79 | 85 | 83 | 69 | 3 | ||
| MIRROR | 77 | 73 | 82 | 82 | 79 | 82 | 5 | |
| RING | 82 | 73 | 78 | 71 | 4 | |||
| SCENE | 83 | 67 | 69 | 78 | 69 | 1 | ||
Из табл. 9.1. видно, что для двух разных ключей GALLERY и HOUSE вычислен одинаковый хеш-адрес, равный 3. Предложен ряд способов разрешения таких коллизий. Рассмотрим один из них, называемый рехешированием.
Перед занесением очередной строки в таблицу проверяем занят ли элемент. Если элемент таблицы свободен, то выполняем занесение. Если же элемент таблицы уже занят, то сравниваем ключи So уже занесенного и Sn заносимого элементов. Если они совпали, то выполняем какую-либо процедуру реагирования на одинаковые ключи и завершаем занесение. Например, для базы данных по кадрам выдаем диагностику о том что информация о данном сотруднике уже есть, для таблицы идентификаторов формируем сообщение о повторном описании и т.п. Если же ключи So и Sn не совпали, то вычисляется новый адрес в таблице по формуле:
| (0.1.1) |
где Hn - исходный хеш-адрес, Pi - некоторое число, L - длина таблицы.
Если этот элемент также оказался занятым, то задается новое значение Pi и по формуле (0.4.26) вычисляется следующий адрес т.д., пока не будет найден некоторый элемент, который либо пуст, либо содержит ключ Sn, либо не будет получен исходный хеш-адрес. В последнем случае работа прекращается из-за переполнения таблицы. Используются несколько основных способов рехеширования [12,]:
Линейное рехеширование.
В этом, наиболее распространенном и простом случае P1 равно 1,
P2 равно 2 и т.д.
Число сравнений E » (1 - V/2)(1-V),
где V - коэффициент заполненности таблицы.
10% - E = 1.06 сравнений,
50% - E = 1.50 сравнений,
90% - E = 5.50 сравнений.
Случайное рехеширование.
При этом способе Pj - псевдослучайное число.
Способ хорош при L = 2m где m - целое.
Число сравнений E » - (1/V)log(1-V).
10% - E = 1.05 сравнений,
50% - E = 1.39 сравнений,
90% - E = 2.56 сравнений.
Рехеширование сложением с выбором.
При этом способе Pi = i ×Hn (i = 1јL-1),.
Способ хорош когда L - простое число.
Квадратичное рехеширование.
При этом способе Pi = A×(i2) + B×i + C.
Здесь A, B, C - произвольные числа, выбор которых определяется
эффективностью вычисления формулы на конкретной машине.
Время вычислений хеш-адреса меньше чем при случайном рехешировании.
Если L - простое число, то E Ј L/2.
Третья форма организации данных - списки, когда логическая и физическая организация данных разделены и для доступа к данным используются указатели на данные.
Далее будем рассматривать структуры данных с использованием списков указателей.
Линейный список - множество элементов с помощью которых свойства структуры задаются посредством линейного (одномерного) относительного расположения элементов. При этом k-й указатель непосредственно находится после (k-1)-го.
С таким списком возможны следующие операции:
Пример линейного списка показан на рис. 0.4.39.
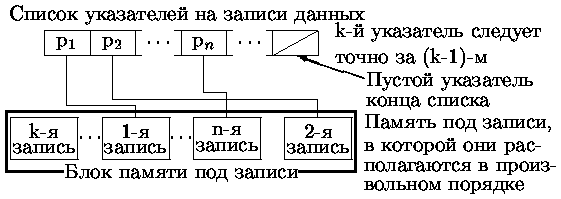
Очевидно, что процесс удаления может приводить к большим перемещениям данных. Пусть, например, надо удалить запись номер 1 (см. рис. 0.4.39). Это потребует удаления указателя p1 и переписи всех далее расположенных указателей на освобождаемое место списка. Аналогичные проблемы возникают и при вставке в требуемое место.
Поэтому естественным шагом является построение так называемых комбинированных списков, содержащих кроме указателей на записи данных также и дополнительные указатели, указывающие на на следующий элемент списка указателей (рис. 0.4.40).
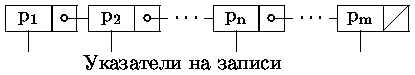
Достоинства таких списков:
· много проще вставка в требуемое место, например, вставка нового элемента между (n-1)-м и n-м сводится к перестройке двух указателей (рис. 0.4.41)

· много проще удаление (рис. 0.4.42), которое сводится к
перестройке трех указателей - одного указателя для собственно
удаления и перестройке двух указателей для включения удаляемого
элемента в список свободной памяти.
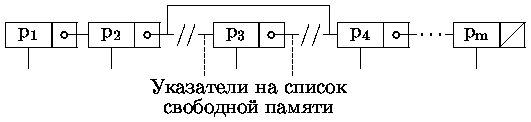
· разделение и соединение списков упрощается,
· возможно формирование сложных структур данных,
· можно надстраивать переменное число списков различных длин,
· любой из элементов списка может быть заголовком некоторого
другого списка, когда указатель на данные указывает на
некоторый другой список,
· за счет использования нескольких указателей возможно формирование подсписков.
Недостатки:
· увеличивается потребность в памяти из-за дополнительных указателей,
· обычно требуемая последовательная обработка замедляется,
· выбор нужного элемента списка требует последовательного прохода по всем предшествующим элементам списка, начиная с начального.
Последнего недостатка лишены списки с указателями не только вперед, на следующий элемент, но и назад, на предшествующий элемент. Эти списки чаще всего используются в виде циклических, когда первый элемент указывает на последний, как предшествующий ему. В свою очередь последний элемент списка как на последующий указывает на начальный элемент. Доступ к началу списка обеспечивает специальный элемент - заголовок списка, который может сопровождаться данными, характеризующими список в целом (рис. 0.4.43). Например, если список представляет собой описание какой-либо фигуры (тела), то дополнительными данными могут быть идентификатор и тип фигуры или иная семантическая информация.
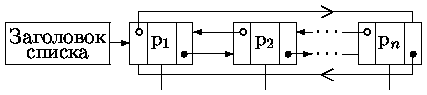
Ясно, что удаление или вставка элемента в таком списке также упрощаются.
Во многих приложениях машинной графики возникает потребность в представлении трехмерных тел (вычислительный эксперимент, автоматизация проектирования, роботизация, вычислительная томография, тренажеры, видеографика и т.д.).
Можно выделить две основные задачи, связанные с представлением трехмерных тел, - построение модели уже существующего объекта и синтез модели заранее не существовавшего объекта.
При решении первой задачи в общем случае может потребоваться задание бесконечного количества координат точек. Чаще же всего объект с той или иной точностью аппроксимируют некоторым конечным набором элементов, например, поверхностей, тел и т.п.
При решении второй задачи, выполняемой чаще всего в интерактивном режиме, основное требование к средствам формирования и представления модели - удобство манипулирования.
Используются три основных типа 3D моделей:
· каркасное представление, когда тело описывается набором ребер,
· поверхностное, когда тело описывается набором ограничивающих
его поверхностей,
· модель сплошных тел, когда тело формируется из отдельных
базовых геометрических и, возможно, конструктивно - технологических
объемных элементов с помощью операций объединения, пересечения,
вычитания и преобразований.
Важно отметить, что 3D системы существенно ориентируются на область приложений так как многие характерные для них задачи, выполняемые программным путем, стоят очень дорого и сильно зависят от выбора возможных моделей. Типичными такими задачами, в частности, являются получение сечений и удаление невидимых частей изображения. Обычно имеется много вариантов реализации различных моделей в б\'ольшей или меньшей степени эффективных в зависимости от различных областей приложений и решаемых задач. Поэтому в 3D системах стремятся использовать многообразие моделей и поддерживать средства перехода от одной модели к другой.
Другим важным обстоятельством является то, что для современных систем характерно стремление моделировать логику работы, принятую пользователем. Это требует наличия средств перехода от модели, удобной для пользователя, к модели удобной для визуализации (модели тел в виде граней).
При формировании 3D модели используются:
· двумерные элементы (точки, прямые, отрезки прямых, окружности
и их дуги, различные плоские кривые и контуры),
· поверхности (плоскости, поверхности, представленные семейством
образующих, поверхности вращения, криволинейные поверхности),
· объемные элементы (параллелепипеды, призмы, пирамиды, конусы,
произвольные многогранники и т.п.).
Из этих элементов с помощью различных операций формируется внутреннее
представление модели.
Используются два основных способа формирования геометрических
элементов моделей - это построение по заданным отношениям
(ограничениям) и построение с использованием преобразований.
Построение с использованием отношений заключается в том, что задаются:
· элемент подлежащий построению,
· список отношений и элементы к которым относятся отношения.
Например, построение прямой, проходящей через точку пересечения двух других прямых и касательную к окружности.
Используется два способа реализации построения по отношениям - общий и частный.
При общем способе реализации построение по заданным отношениям можно представить в виде двухшаговой процедуры:
· на основе заданных типов отношений, элементов и параметров
строится система алгебраических уравнений,
· решается построенная система уравнений.
Очевидное достоинство такого способа - простота расширения системы - для введения нового отношения достаточно просто написать соответствующие уравнения.
Основные проблемы такого способа заключаются в следующем:
· построенная система уравнений может иметь несколько решений,
поэтому требуется выбрать одно из них, например, в диалоговом
режиме,
· система уравнений может оказаться нелинейной, решаемой
приближенными методами, что может потребовать диалога для выбора
метода(ов) приближенного решения.
В связи с отмеченными проблемами общий подход реализован только в наиболее современных системах и при достаточно высоком уровне разработчиков в области вычислительной математики [8].
Большинство же систем реализует частный подход, первым приходящий в голову и заключающийся в том, что для каждой триады, включающей строящийся элемент, тип отношения и иные элементы, затрагиваемые отношением, пишется отдельная подпрограмма (например построение прямой, касательной к окружности в заданной точке). Требуемое построение осуществляется выбором из меню и тем или иным вводом требуемых данных [6,].
Преимущества такого подхода ясны - проще писать систему. Не менее очевидны и недостатки, когда пользователю требуется использовать сильно разветвленные меню и/или запоминать мало вразумительные сокращения или пиктограммы, так как обычно число требуемых вариантов построения исчисляется сотнями. Расширение системы, реализуемое добавлением новой подпрограммы, требует ее перепроектирования, по крайней мере в части обеспечения доступа пользователя к новым возможностям. В некотором смысле предельный пример этого подхода - система AutoCAD фирмы Autodesk. Авторы даже гордятся сложностью системы: "AutoCAD предоставляет эту крайне сложную технологию" (Предисловие к Справочному руководству AutoCAD версии 2.5).
Понятно, что перспективы за общим подходом с разумным использованием частных решений. Вместе с тем устаревшие системы типа AutoCad скорее всего также будут продолжать использоваться в силу распространенности, сложившегося круга обученных пользователей и т.п.
Построение нового объекта с использованием преобразований заключается в следующем:
· задается преобразуемый объект,
· задается преобразование (это может быть обычное аффинное
преобразование, определяемое матрицей, или некоторое деформирующее
преобразование, например, замена одного отрезка контура ломаной),
· выполнение преобразования; в случае аффинного преобразования для
векторов всех характерных точек преобразуемого объекта выполняется
умножение на матрицу; для углов вначале переходят к точкам и затем
выполняют преобразование.
Важное значение при формировании как 2D, так и 3D моделей имеет построение элементарных кривых. Кривые строятся, в основном, следующими способами:
· той или иной интерполяцией по точкам,
· вычислением конических сечений,
· расчетом пересечения поверхностей,
· выполнением преобразования некоторой кривой,
· формированием замкнутых или разомкнутых контуров из отдельных
сегментов, например, отрезков прямых, дуг конических сечений или
произвольных кривых.
В качестве последних обычно используются параметрические кубические кривые, так как это наименьшая степень при которой обеспечиваются:
· непрерывность значения первой (второй) производной в точках
сшивки сегментов кривых,
· возможность задания неплоских кривых.
Параметрическое представление кривых выбирается по целому ряду причин, в том числе потому, что зачастую объекты могут иметь вертикальные касательные. При этом аппроксимация кривой y = f(x) аналитическими функциями была бы невозможной. Кроме того кривые, которые надо представлять, могут быть неплоскими и незамкнутыми. Наконец, параметрическое представление обеспечивает независимость представления от выбора системы координат и соответствует процессу их отображения на устройствах: позиция естественным образом определяется как две функции времени x(t) и y(t).
В общем виде параметрические кубические кривые можно представить в форме:
| (0.2.2) |
где параметр t можно считать изменяющимся в диапазоне от 0 до 1, так как интересуют конечные отрезки.
Существует много методов описания параметрических кубических кривых. К наиболее применяемым относятся:
· метод Безье, широко используемый в интерактивных приложениях;
в нем задаются положения конечных точек кривой, а значения первой
производной задаются неявно с помощью двух других точек, обычно не
лежащих на кривой;
· метод В-сплайнов, при котором конечные точки не лежат на
кривой и на концах сегментов обеспечивается непрерывность первой и
второй производных.
В форме Безье кривая в общем случае задается в виде полинома Бернштейна:
|
где Pi - значения координат в вершинах ломаной, используемой в качестве управляющей ломаной для кривой, t - параметр,
|
При этом крайние точки управляющей ломаной и кривой совпадают, а наклоны первого и последнего звеньев ломаной совпадают с наклоном кривой в соответствующих точках.
Предложены различные быстрые схемы для вычисления кривой Безье.
В более общей форме B-сплайнов кривая в общем случае задается соотношением:
|
где Pi - значения координат в вершинах ломаной, используемой в качестве управляющей ломаной для кривой, t - параметр, Nim - весовые функции, определяемые рекуррентным соотношением:
|
|
Используются и многие другие методы, например, метод Эрмита, при котором задаются положения конечных точек кривой и значения первой производной в них.
Общее в упомянутых подходах состоит в том, что искомая кривая строится с использованием набора управляющих точек.
Основные способы построения поверхностей:
· интерполяцией по точкам,
· перемещением образующей кривой по заданной траектории
(кинематический метод),
· деформацией исходной поверхности,
· построением поверхности эквидистантной к исходной,
· кинематический принцип,
· операции добавления/удаления в структуре,
· теоретико-множественные (булевские) операции.
Широко используется бикубические параметрические куски, с помощью которых сложная криволинейная поверхность аппроксимируется набором отдельных кусков с обеспечением непрерывности значения функции и первой (второй) производной при переходе от одного куска к другому. В общем случае представление бикубического параметрического куска имеет вид (приведена формула для x-координаты, для других координат формула аналогична):
|
Аналогично случаю с параметрическими кубическими кривыми, наиболее применимыми являются:
· форма Безье,
· форма В-сплайнов,
· форма Эрмита.
Как уже отмечалось, можно выделить два основных типа представлений 3D моделей:
· граничное, когда в модели хранятся границы объекта, например,
вершины, ребра, грани,
· в виде дерева построения, когда хранятся базовые объекты
(призма, пирамида, цилиндр, конус и т.п.) из которых формировалось
тело и использованные при этом операции; в узле дерева сохраняется
операция формирования, а ветви представляют объекты.
Предельным случаем граничной модели является модель, использующая перечисление всех точек занимаемого ею пространства. В частности, тело может быть аппроксимировано набором "склеенных" друг с другом параллелепипедов, что может быть удобно для некоторых вычислений (веса, объемы, расчеты методом конечных элементов и т.д.).
Часто используются гибридные модели, в которых в различной мере смешиваются эти два основных типа представления. В частности, в граничной модели может сохраняться информация о способе построения, например, информация о контуре и траектории его перемещения для формирования заданной поверхности (это т.н. кинематические модели). В моделях в виде дерева построения в качестве элементарных могут использоваться не только базовые объекты, но также и сплошные тела, заданные с помощью границ.
В общем случае нельзя утверждать, что одна модель во всем лучше другой. Так, например, граничная модель удобна для выполнения операций визуализации (удаление невидимых частей, закраска и т.п.), с другой стороны модель в виде дерева построения естественным образом может обеспечить параметризацию объекта, т.е. модификацию объекта изменением тех или иных отдельных параметров, вплоть до убирания каких-либо составных частей, но не удобна для визуализации, так как требует перевычисления объекта по дереву построения. Поэтому необходимы средства взаимного преобразования моделей. Понятно, что из более общей можно сформировать более простую, обратное преобразование далеко не всегда возможно или целесообразно, что и иллюстрируется сплошными и штриховыми линиями на рис. 0.5.44.
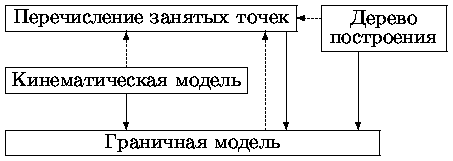
Из рис. 0.5.44 видно особое место граничной модели, преобразование в которую возможно из любых других1. Учитывая это, а также и то, что эта модель наиболее удобна для визуализации дальнейшее рассмотрение будет, в основном, относиться к этой модели.
Используются две основных разновидности способов представления поверхностей тела:
· представление в виде набора вершин, ребер и плоских
многоугольников (полигональных сеток),
· представление с использованием параметрических бикубических
площадок (кусков).
Полигональные сетки используются как для представления плоских поверхностей, так и для аппроксимации криволинейных, в том числе и параметрических бикубических площадок, поэтому далее в основном подразумевается представление поверхности в виде плоских многоугольников.
Как отмечалось, полигональная сетка представляет собой набор вершин, ребер и плоских многоугольников. Вершины соединяются ребрами. Многоугольники рассматриваются либо как последовательность вершин или ребер. Можно предложить много способов внутреннего представления полигональных сеток.
На рис. 0.5.45 изображен простой пример полигональной сетки из четырех многоугольников с девятью вершинами и двенадцатью ребрами. На рис. 0.5.46-0.5.48 рассмотрены несколько различных представлений и приведены соображения по их эффективности и удобству манипулирования.
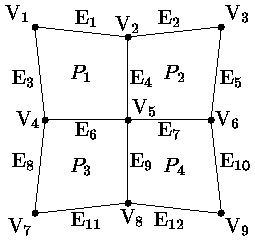

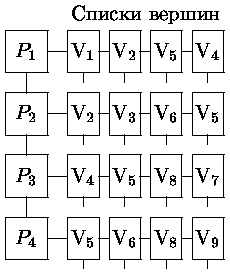
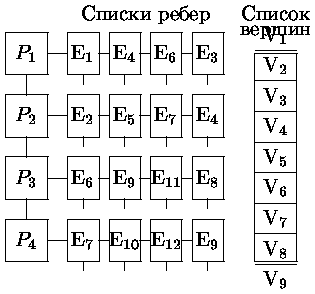
· объемная модель,
· полиэдральная модель,
· упрощенные модели,
· сосуществование моделей.
Процедурная модель и представление в данных.
Методы удаления невидимых частей сцены можно классифицировать:
Применение - векторные устройства. Могут применяться и в растровых для ускорения процесса визуализации, но при этом не используется основное ценное качество растрового дисплея - возможность закраски поверхностей.
Наиболее известный ранний алгоритм - алгоритм Робертса (1963 г.). Работает с только выпуклыми телами в пространстве объектов. Каждый объект сцены представляется многогранным телом, полученным в результате пересечения плоскостей. Т.е. тело описывается списком граней, состоящих из ребер, которые в свою очередь образованы вершинами.
Вначале из описания каждого тела удаляются нелицевые плоскости, экранированные самим телом. Затем каждое из ребер сравнивается с каждым телом для определения видимости или невидимости. Т.е. объем вычислений растет как квадрат числа объектов в сцене. Наконец вычисляются новые ребра, полученные при протыкании телами друг друга.
Алгоритм предложен Эдом Кэтмулом и представляет собой обобщение буфера кадра. Обычный буфер кадра хранит коды цвета для каждого пиксела в пространстве изображения. Идея алгоритма состоит в том, чтобы для каждого пиксела дополнительно хранить еще и координату Z или глубину. При занесении очередного пиксела в буфер кадра значение его Z-координаты сравнивается с Z-координатой пиксела, который уже находится в буфере. Если Z-координата нового пиксела больше, чем координата старого, т.е. он ближе к наблюдателю, то атрибуты нового пиксела и его Z-координата заносятся в буфер, если нет, то ни чего не делается.
Этот алгоритм наиболее простой из всех алгоритмов удаления невидимых поверхностей, но требует большого объема памяти. Данные о глубине для реалистичности изображения обычно достаточно иметь с разрядностью порядка 20 бит. В этом случае при изображении нормального телевизионного размера в 768×576 пикселов для хранения Z-координат необходим объем памяти порядка 1 Мбайта. Суммарный объем памяти при 3 байтах для значений RGB составит более 2.3 Мбайта.
Время работы алгоритма не зависит от сложности сцены. Многоугольники, составляющие сцену, могут обрабатываться в произвольном порядке. Для сокращения затрат времени нелицевые многоугольники могут быть удалены. По сути дела алгоритм с Z-буфером - некоторая модификация уже рассмотренного алгоритма заливки многоугольника. Если используется построчный алгоритм заливки, то легко сделать пошаговое вычисление Z-координаты очередного пиксела, дополнительно храня Z-координаты его вершин и вычисляя приращение dz Z-координаты при перемещении вдоль X на dx, равное 1. Если известно уравнение плоскости, в которой лежит обрабатываемый многоугольник, то можно обойтись без хранения Z-координат вершин. Пусть уравнение плоскости имеет вид:
|
Тогда при C не равном нулю
|
Найдем приращение Z-координаты пиксела при шаге по X на dx, помня, что Y очередной обрабатываемой строки - константа.
|
но dx = 1, поэтому
|
Основной недостаток алгоритма с Z-буфером - дополнительные затраты памяти. Для их уменьшения можно разбивать изображение на несколько прямоугольников или полос. В пределе можно использовать Z-буфер в виде одной строки. Понятно, что это приведет к увеличению времени, так как каждый прямоугольник будет обрабатываться столько раз, на сколько областей разбито пространство изображения. Уменьшение затрат времени в этом случае может быть обеспечено предварительной сортировкой многоугольников на плоскости.
Другие недостатки алгоритма с Z-буфером заключаются в том, что так как пикселы в буфер заносятся в произвольном порядке, то возникают трудности с реализацией эффектов прозрачности или просвечивания и устранением лестничного эффекта с использованием предфильтрации, когда каждый пиксел экрана трактуется как точка конечного размера и его атрибуты устанавливаются в зависимости от того какая часть пиксела изображения попадает в пиксел экрана. Но другой подход к устранению лестничного эффекта, основанный на постфильтрации - усреднении значений пиксела с использованием изображения с большим разрешением реализуется сравнительно просто за счет увеличения расхода памяти (и времени). В этом случае используются два метода. Первый состоит в том, что увеличивается разрешение только кадрового буфера, хранящего атрибуты пикселов, а разрешение Z-буфера делается совпадающим с размерами пространства изображения. Глубина изображения вычисляется только для центра группы усредняемых пикселов. Это метод неприменим, когда расстояние до наблюдателя имитируется изменением интенсивности пикселов. Во втором методе и кадровый и Z буфера имеют увеличенное разрешение и усредняются атрибуты пиксела, так и его глубина.
Общая схема алгоритма с Z-буфером:
· Инициализировать кадровый и Z-буфера. Кадровый буфер закрашивается фоном. Z-буфер закрашивается минимальным значением Z.
· Выполнить преобразование каждого многоугольника сцены в растровую форму. При этом для каждого пиксела вычисляется его глубина z. Если вычисленная глубина больше, чем глубина, уже имеющаяся в Z-буфере, то занести в буфера атрибуты пиксела и его глубину, иначе никаких занесений не выполнять.
· Выполнить, если это было предусмотрено, усреднение изображения с понижением разрешения.
Рассмотрим теперь алгоритм с Z-буфером размером в одну строку, который представляет собой обобщение алгоритма построчной заливки многоугольника, представленный в процедурах V_FP0 и V_FP1 в приложениях. Модификация должна учесть то, что для каждой строки сканирования теперь может обрабатываться не один многоугольник.
Общая схема такого алгоритма следующая:
Алгоритм работает в пространстве изображения и анализирует область на экране дисплея (окно) на наличие в них видимых элементов. Если в окне нет изображения, то оно просто закрашивается фоном. Если же в окне имеется элемент, то проверяется достаточно ли он прост для визуализации. Если объект сложный, то окно разбивается на более мелкие, для каждого из которых выполняется тест на отсутствие и/или простоту изображения. Рекурсивный процесс разбиения может продолжаться до тех пор пока не будет достигнут предел разрешения экрана.
Можно выделить 4 случая взаимного расположения окна и многоугольника
(рис. 0.6.49):
· многоугольник целиком вне окна,
· многоугольник целиком внутри окна,
· многоугольник пересекает окно,
· многоугольник охватывает окно.
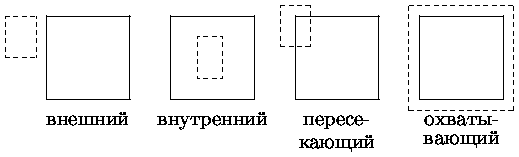
В четырех случаях можно сразу принять решение о правилах закраски области экрана:
· все многоугольники сцены - внешние по отношению к окну. В этом случае окно закрашивается фоном;
· имеется всего один внутренний или пересекающий многоугольник. В этом случае все окно закрашивается фоном и затем часть окна, соответствующая внутреннему или пересекающему окну закрашивается цветом многоугольника;
· имеется единственный охватывающий многоугольник. В этом случае окно закрашивается его цветом.
· имеется несколько различных многоугольников и хотя бы один из них охватывающий. Если при этом охватывающий многоугольник расположен ближе остальных к наблюдателю, то окно закрашивается его цветом.
В любых других случаях процесс разбиения окна продолжается. Легко видеть, что при растре 1024×1024 и делении стороны окна пополам требуется не более 10 разбиений. Если достигнуто максимальное разбиение, но не обнаружено ни одного из приведенных выше четырех случаев, то для точки с центром в полученном минимальном окне (размером в пиксел) вычисляются глубины оставшихся многоугольников и закраску определяет многоугольник, наиболее близкий к наблюдателю. При этом для устранения лестничного эффекта можно выполнить дополнительные разбиения и закрасить пиксел с учетом всех многоугольников, видимых в минимальном окне.
Первые три случая идентифицируются легко. Последний же случай фактически сводится к поиску охватывающего многоугольника, перекрывающего все остальные многоугольники, связанные с окном. Проверка на такой многоугольник может быть выполнена следующим образом: в угловых точках окна вычисляются Z-координаты для всех многоугольников, связанных с окном. Если все четыре такие Z-координаты охватывающего многоугольника ближе к наблюдателю, чем все остальные, то окно закрашивается цветом соответствующего охватывающего многоугольника. Если же нет, то мы имеем сложный случай и разбиение следует продолжить.
Очевидно, что после разбиения окна охватывающие и внешние многоугольники наследуются от исходного окна. Поэтому необходимо проверять лишь внутренние и пересекающие многоугольники.
Из изложенного ясно, что важной частью алгоритма является определение расположения многоугольника относительно окна.
Проверка на то что многоугольник внешний или внутренний относительно окна для случая прямоугольных окон легко реализуется использованием прямоугольной оболочки многоугольника и сравнением координат. Для внутреннего многоугольника должны одновременно выполняться условия:
|
| здесь | Xmin,Xmax,Ymin,Ymax | - | ребра оболочки |
| Wл, Wп, Wн, Wв | - | ребра окна |
Для внешнего многоугольника достаточно выполнение любого из следующих условий:
|
Таким способом внешний многоугольник, охватывающий угол окна не будет идентифицирован как внешний (см. рис. 0.6.50).
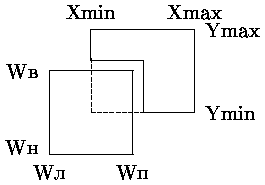
Проверка на пересечение окна многоугольником может быть выполнена проверкой на расположение всех вершин окна по одну сторону от прямой, на которой расположено ребро многоугольника. Пусть ребро многоугольника задано точками P1(x1,y1,z1) и P2(x2,y2,z2), а очередная вершина окна задается точкой P3(x3,y3,z3). Векторное произведение вектора P1P3 на вектор P1P2, равное (x3-x1)(y2-y1) - (y3-y1)(x2-x1) будет меньше 0, равно 0 или больше 0, если вершина лежит слева, на или справа от прямой P1P2. Если знаки различны, то окно и многоугольник пересекаются. Если же все знаки одинаковы, то окно лежит по одну сторону от ребра, т.е. многоугольник может быть либо внешним, либо охватывающим.
Вернемся к примеру 0.6.50. Такой многоугольник рассмотренными тестами не был идентифицирован ни как внутренний ни как пересекающий. Т.е. он может быть либо внешним, либо охватывающим. Для завершающей классификации может использоваться тест с подсчетом угла, рассматривавшийся ранее для определения нахождения точки внутри/вне многоугольника. В этом тесте вычисляется суммарный угол, на который повернется луч, исходящий из некоторой точки окна (обычно центра), при последовательном обходе вершин многоугольника.
Если суммарный угол равен 0, то многоугольник - внешний. Если же угол равен N×360°, то многоугольник охватывает окно N раз. Простейшая иллюстрация этого теста приведена на рис. 0.6.51.
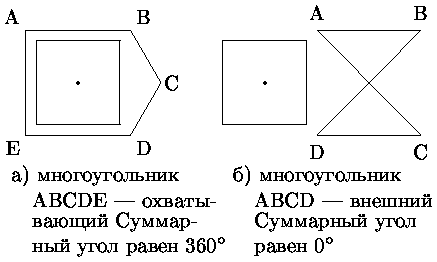
В алгоритмах построчного сканирования результирующее изображение генерируется построчно причем, подобно ранее рассмотренному алгоритму построчной заливки многоугольника, используется связность соседних растровых строк изображения. Отличие состоит в том, что учитываются все, а не один многоугольник.
Алгоритм работает в пространстве изображения с окном высотой в одну строку и шириной в экран, тем самым трехмерная задача сводится к двумерной.
Последовательность шагов алгоритма:
· построение списка ребер,
· построение списка многоугольников,
· построение списка активных ребер - создается таблица ребер, включающая все негоризонтальные ребра многоугольников, причем элементы таблицы по значению Y-координаты отсортированы по группам.
При рассмотрении этого алгоритма предполагается, что наблюдатель находится на положительной полуоси Z, а экран дисплея перпендикулярен оси Z и располагается между объектом и наблюдателем.
Удаление невидимых (скрытых) поверхностей в алгоритме трассировки
лучей выполняется следующим образом:
· сцена преобразуется в пространство изображения,
· из точки наблюдения в каждый пиксел экрана проводится луч и определяется какие именно объекты сцены пересекаются с лучом,
· вычисляются и упорядочиваются по Z координаты точек пересечения объектов с лучом. В простейшем случае для непрозрачных поверхностей без отражений и преломлений видимой точкой будет точка с максимальным значением Z-координаты. Для более сложных случаев требуется сортировка точек пересечения вдоль луча.
Ясно, что наиболее важная часть алгоритма - процедура определения пересечения, которая в принципе выполняется Rx×Ry×N раз (здесь Rx,Ry - разрешение дисплея по X и Y, соответственно, а N - количество многоугольников в сцене).
Очевидно, что повышение эффективности может достигаться сокращением времени вычисления пересечений и избавлением от ненужных вычислений. Последнее обеспечивается использованием геометрически простой оболочки, объемлющей объект - если луч не пересекает оболочку, то не нужно вычислять пересечения с ним многоугольников, составляющих исследуемый объект.
При использовании прямоугольной оболочки определяется преобразование, совмещающее луч с осью Z. Оболочка подвергается этому преобразованию, а затем попарно сравниваются знаки Xmin с Xmax и Ymin с Ymax. Если они различны, то есть пересечение луча с оболочкой (см. рис. 0.6.52)
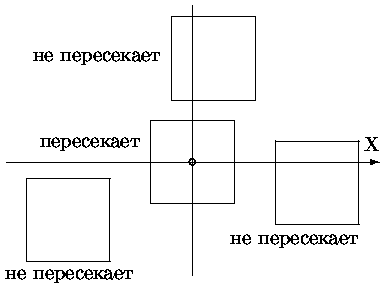
При использовании сферической оболочки для определения пересечения луча со сферой достаточно сосчитать расстояние от луча до центра сферы. Если оно больше радиуса, то пересечения нет. Параметрическое уравнение луча, проходящего через две точки P1(x1,y1,z1) и P2(x2,y2,z2), имеет вид:
|
Минимальное расстояние от точки центра сферы P0(x0,y0,z0) до луча равно:
|
Этому соответствует значение t:
|
Если d2 > R2, то луч не пересекает объекты, заключенные в оболочку.
Дальнейшее сокращение расчетов пересечений основывается на использовании групп пространственно связанных объектов. Каждая такая группа окружается общей оболочкой. Получается иерархическая последовательность оболочек, вложенная в общую оболочку для всей сцены. Если луч не пересекает какую-либо оболочку, то из рассмотрения исключаются все оболочки, вложенные в нее и, следовательно, объекты. Если же луч пересекает некоторую оболочку, то рекурсивно анализируются все оболочки вложенные в нее.
Наряду с вложенными оболочками для сокращения расчетов пересечений используется отложенное вычисление пересечений с объектами. Если обнаруживается, что объект пересекается лучом, то он заносится в специальный список пересеченных. После завершения обработки всех объектов сцены объекты, попавшие в список пересеченных упорядочиваются по глубине. Заведомо невидимые отбрасываются а для оставшихся выполняется расчет пересечений и отображается точка пересечения наиболее близкая к наблюдателю.
Дополнительное сокращение объема вычислений может достигаться отбрасыванием нелицевых граней, учетов связности строк растрового разложения и т.д.
Для сокращения времени вычислений собственно пересечений предложено достаточно много алгоритмов, упрощающих вычисления для определенной формы задания поверхностей.
Где нужен реализм:
· в конструировании,
· в архитектуре,
· в биологии и медицине,
· в науке (компьютерное моделирование),
· в масс-медиа,
· в тренажерах, играх.
Основные направления:
· синтез реалистичных изображений,
· реалистическое оживление синтезированных объектов.
С точки зрения приложений в науке и промышленности наиболее важно
первое направление.
Ключевая проблема - реалистическое представление освещенности:
· модели освещения, прозрачность, тени, фактура,
· глобальная модель освещения с трассировкой лучей,
· излучательность.
Диффузное отражение света точечного источника от идеального рассеивателя определяется по закону Ламберта, согласно которому падающий свет рассеивается во все стороны с одинаковой интенсивностью. В этом случае освещенность точки пропорциональна доле ее площади, видимой от источника.
|
где Ir - интенсивность отраженного света, Ip - интенсивность точечного источника, 0 Ј Pd Ј 1 - коэффициент диффузного отражения, зависящий от материала поверхности и длины волны, 0 Ј f Ј p/2 - угол между направлением света и нормалью к поверхности.
В реальных сценах, кроме света от точечных источников, присутствует и рассеянный свет, который упрощенно учитывается с помощью коэффициента рассеяния:
|
где Ir - интенсивность рассеянного света, 0 Ј Pr Ј 1 - коэффициент диффузного отражения рассеянного света.
Субъективно достаточно реалистичный учет расстояния от центра проекции до объекта обеспечивается линейным затуханием:
|
где d - расстояние от центра проекции до объекта, а K - произвольная константа.
При параллельной проекции, когда точка наблюдения находится в бесконечности, учет расстояния обеспечивается тем, что объект, ближайший к точке наблюдения, освещается полностью, далее расположенные - с уменьшенной освещенностью и в качестве d берется расстояние от объекта ближайшего к наблюдателю.
Свет, отраженный от идеального зеркала, виден только если угол между направлениями наблюдения и отражения равен нулю. Для неидеальных отражающих поверхностей используется модель Фонга [27]:
|
где W(l, f) - кривая отражения, зависящая от длины волны l света источника и угла падения f, -p/1 Ј a Ј p/2 - угол между направлениями наблюдения и отражения, 1 Ј n Ј 200 - показатель степени, определяющий убывание интенсивности при изменении угла.
Часто W(l, f) заменяется константой Ks, такой чтобы полученная картина была субъективно приемлема.
Суммарная модель освещения имеет вид:
|
Или при использовании вместо W(l, f) константы Ks:
|
Если использовать нормированные вектора направлений падения L, нормали N, отражения R и наблюдения V, то модель освещения для одного источника принимает вид:
|
Если источник света находится бесконечности, то для данного плоского многоугольника L·N равно константе, а R·V меняется в пределах многоугольника. Для поверхностей, представленных например в виде бикубических кусков, каждое произведение меняется в пределах куска. Так как эти вычисления требуется производить для каждого пиксела строки, то вычислительные затраты могут быть очень велики. Фонг предложил алгоритм пошагового вычисления по рассмотренной модели, существенно снижающий затраты.
Кроме эмпирической модели освещенности Фонга используются модели, представляющие отражающую поверхность в виде плоских микроскопических граней. Ориентации нормалей к граням относительно нормали к средней линии поверхности задаются некоторым распределением, например, Гаусса.
Существует три основных способа закраски многоугольников: однотонная закраска, закраска с интерполяцией интенсивности и закраска с интерполяцией векторов нормали.
При однотонной закраске предполагается, что и источник света и наблюдатель находятся в бесконечности, поэтому произведения L·N и R·V постоянны. На изображении могут быть хорошо заметны резкие перепады интенсивности между различно закрашенными многоугольниками. Если многоугольники представляют собой результат аппроксимации криволинейной поверхности, то изображение недостаточно реалистично.
В методе закраски с интерполяцией интенсивности (метод Гуро) нормали в вершинах многоугольников вычисляются как результат усреднения нормалей ко всем полигональным граням, которым принадлежит данная вершина. Используя значения нормалей, вычисляют интенсивности в вершинах по той или иной модели освещения. Эти значения затем используются для билинейной интерполяции: для данной строки сканирования вначале находят значения интенсивностей на ребрах, а затем линейно интерполируют между ними при закраске вдоль строки.
В методе закраски с интерполяцией нормали (метод Фонга) значение нормали вдоль строки интерполируется между значениями нормалей на ребрах для данной строки. Значения нормалей на ребрах получается как результат интерполирования между вершинами. Значения же нормалей в вершинах являются результатом усреднения, как и выше рассмотренном методе. Значение нормали для каждого из пикселов строки используется для вычислений по той или иной модели освещения.
В простейшей модели прозрачности преломление не учитывается. При расчетах по такой модели могут использоваться любые алгоритмы удаления невидимых поверхностей, учитывающие порядок расположения многоугольников. При использовании построчных алгоритмов если передний многоугольник оказывается прозрачным, то определяется ближайший из оставшихся, внутри которых находится строка сканирования. Суммарная закраска определяется следующим образом:
|
где 0 Ј k Ј 1 - характеризует прозрачность ближнего многоугольника. Если k = 1, то он непрозрачен. Если же k = 0, то ближний многоугольник полностью прозрачен; Iб - интенсивность для пиксела ближнего многоугольника, Iд - дальнего.
Простой способ определения объектов, попавших в тень и, следовательно, неосвещенных, аналогичен алгоритму удаления невидимых поверхностей: те объекты, которые невидимы из источника освещения, но видимы из точки зрения находятся в тени. На первом шаге в алгоритме с учетом тени определяются все многоугольники, видимые из точки освещения. Затем выполняется удаление поверхностей невидимых из точки зрения. При выполнении закраски многоугольника проверяется не закрыт ли он многоугольником, видимым из источника освещения. Если да, то в модели освещения учитываются (если надо) все три компоненты - диффузное и зеркальное отражения и рассеянный свет. Если же перекрытия нет, то закрашиваемый многоугольник находится в тени и надо учитывать только рассеянный свет.
Решение в лоб - представление в виде соответствующего (очень большого) количества многоугольников мало приемлемо. Более практичное решение - "натягивание" массива узора, полученного в результате оцифровки изображения реальной поверхности на раскрашиваемую. При этом значения из массива узора используются для масштабирования диффузной компоненты в модели освещения.
Для устранения лестничного эффекта должны учитываться все элементы узора, затрагивающие обрабатываемый пиксел изображения.
Такой метод влияет на раскраску поверхности, но оставляет ее гладкой. Неровности могут моделироваться возмущениями нормали поверхности. Другой способ, используемый при синтезе картин - метод фрактальной геометрии.
Метод трассировки лучей используется не только для удаления невидимых частей, но, в основном, для получения высокореалистичных изображений с учетом отражений и преломлений света.
Прямой трассировкой лучей называется процесс расчета освещения сцены с испусканием от всех источников лучей во всех направлениях. При попадании на какой-либо объект сцены луч света может преломившись уйти внутрь тела или отразившись далее продолжить прямолинейное распространение до попадания на следующий объект и так далее. Следовательно, каждая точка сцены может освещаться либо напрямую источником, либо отраженным светом. Часть лучей в конце концов попадет в глаз наблюдателя и сформирует в нем изображение сцены.
Понятно, что вычисления, необходимые для трассировки всех лучей для всех источников и поверхностей слишком объемисты. Причем существенный вклад в полученное изображение внесет лишь небольшая часть оттрассированных лучей.
Для избавления от излишних вычислений используется обратная трассировка, в которой вычисляются интенсивности только лучей, попавших в глаз наблюдателя. В простейшей реализации обратной трассировки отслеживаются лучи, проходящие из глаза наблюдателя через каждый пиксел экрана в сцену. На каждой поверхности сцены, на которую попадает луч, в общем случае формируются отраженный и преломленный лучи. Каждый из таких лучей отслеживается, чтобы определить пересекаемые поверхности. В результате для каждого пиксела строится дерево пересечений. Ветви такого дерева представляют распространение луча в сцене, а узлы - пересечения с поверхностями в сцене. Окончательная закраска определяется прохождением по дереву и вычислением вклада каждой пересеченной поверхности в соответствии с используемыми моделями отражения. При этом различают и обычно по-разному рассчитывают первичную освещенность, непосредственно получаемую от источников света, и вторичную освещенность, получаемую от других объектов.
Сцену можно представить как набор поверхностей, обменивающихся лучистой энергией. Большинство реальных поверхностей является диффузными отражателями, когда падающий луч отражается или рассеивается во всех направлениях полусферы, находящейся над отражающей поверхностью. Особый здесь случай - отражение Ламберта (идеальная диффузия). Метод излучательности описывает баланс энергетического равновесия в замкнутой системе. Предполагается что поверхности идеально диффузны, т.е. после отражения падающий луч пропадает. Излучательность отдельной поверхности включает самоизлучение и отраженный или пропущенный свет.
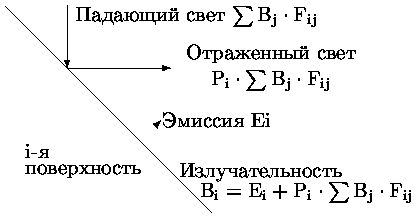
Ei = [Энергия/ ед.площади ·ед.времени] - эмиссия,
Pi - безразмерный коэффициент отражения,
Bi - полный уровень света, исходящего от поверхности
Fij - форм-фактор - часть энергии, исходящая от одной поверхности и достигающая другой
Если поверхности сцены разделены на n элементов, имеющих постоянную излучательность, то взаимодействие потоков света в сцене описывается системой уравнений:
|
Эта система уравнений решается итерационным методом с выбором в качестве начального приближения для излучательности эмиссии поверхности:
Bi0 = Ei,
и последующих приближений вида:
Bik+1 = Ei + Pi еj = 1n Fij Bjk.
После определения излучательности каждого фрагмента производится вычисление излучательностей вершин таким образом, чтобы при билинейной интерполяции в пределах каждого фрагмента была обеспечена непрерывность закраски на границах.
Для этого в каждом многоугольнике значения излучательности для внутренних относительно многоугольника вершин фрагментов вычисляются как среднее значение излучательностей фрагментов, окружающих вершину (рис. 0.7.54). Определения излучательности внешних вершин выполняют экстраполяцией средних значений в смежных внутренних вершинах (см. рис. 0.7.54).
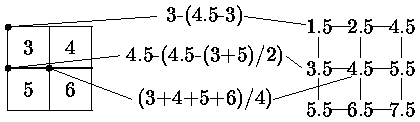
Формирование результирующего изображения выполняется после выбора требуемой точки наблюдения и проецирования сцены на картинную плоскость. Видно, что этот метод не зависит от точки наблюдения. При выводе определяется какой фрагмент отображается в каждом пикселе экрана. При этом используются z-буфер и кадровый буфер. Пересечение линии, соединяющей глаз и пиксел с плоскостью фрагмента, позволяет найди координату точки, отображаемую в текущий пиксел. Координата пересечения (x, y, z) преобразуется в координаты (u, v) на фрагменте. После этого значения излучательностей вершин используются при билинейной интерполяции трех значений излучательностей в пределах каждого фрагмента (рис. 0.7.55).
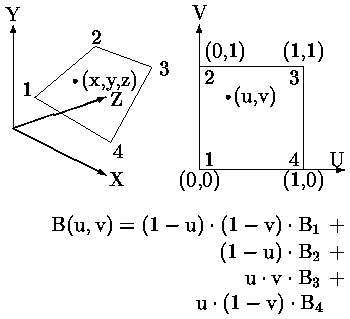
Наиболее трудоемкая часть метода излучательности - вычисление форм факторов.
Для двух неперекрытых элементарных площадок i и j форм-фактор определяет часть световой энергии, исходящей из одной площадки на другую, и имеет вид:
|
где r - расстояние между элементами dAi и dAj, fi и fj - углы между нормалями к элементам и соединяющим их отрезком (рис. 0.7.56).
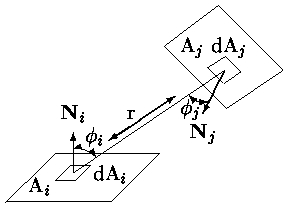
Интегрируя по площади dAj получаем форм-фактор конечного элемента площади Aj относительно элементарной площадки dAi:
|
Выражение для форм-фактора между двух конечных неперекрытых площадок определяется как средняя площадь:
|
Взаимное перекрытие может быть учтено с помощью функции Hij, принимающей значение от 0 до 1 в зависимости от степени перекрытия площадки Aj площадкой Ai:
|
Вычисление этого интеграла, как правило, затруднено. Для его вычисления предложен т.н. алгоритм полукуба. Основная идея которого состоит в том, что если два любых фрагмента в пространстве после проецирования на полусферу заняли на ней одну и ту же площадь и место, то их формфакторы будут одинаковы. Это утверждение справедливо и при проецировании на любую другую окружающую поверхность, в том числе куб.
Куб строится таким образом, чтобы центр фрагмента, принимающего отраженные световые потоки, совпал с центром куба, а нормаль к фрагменту в этой точке примем за положительное направление оси Z. В этом случае полусфера заменяется верхней частью куба (полукубом). Разобьем плоскости полукуба на квадратные пикселы. Спроектируем все пространство на пять плоскостей полукуба при этом производится отсечение по пирамиде видимости с центром в центре куба. Если два фрагмента сцены проецируются на один и тот писел куба,
Здесь приведены тексты соответствующих процедур с пояснениями и тестовая программа. Процедуры позволяют генерировать вектора в любом квадранте с использованием алгоритмов несимметричного цифрового дифференциального анализатора и Брезенхема, а также построения ребра, ограничивающего заполненный многоугольник, модифицированным алгоритмом Брезенхема, уменьшающим лестничный эффект.
Предусмотрена возможность задания атрибутов формируемых отрезков - номер цвета и размер пиксела, используемого при формировании отрезков.
В тестовой программе предусмотрено, что при наличии SVGA-адаптера он может использоваться как в обычном режиме, так и в режиме до 1024x768 точек с 256 цветами.
/*------------------------------------------------- V_VECTOR.C
* Подпрограммы генерации векторов
*/
#include <graphics.h>
#include <stdio.h>
#define PutMay putpixel
static int Pix_X= 3, /* Размер пиксела по X */
Pix_Y= 3, /* Размер пиксела по Y */
Pix_C= 64, /* Нач. индекс цвета пиксела */
Pix_V= 64; /* Количество оттенков */
/*--------------------------------------------------- PutPixLn
* Подпрограмма заносит "кpупный" пиксел в позицию X,Y
* Точка (0, 0) - левый верхний угол экрана.
* Размеры пиксела задается фактическими паpаметpами x и y.
* Hомер оттенка пиксела задается фактическим паpаметpом c.
*/
void PutPixLn (int x, int y, int c)
{ int ii, jj, kk;
x *= Pix_X; y *= Pix_Y;
ii= Pix_Y;
while (--ii >= 0) {
jj= Pix_X; kk= x;
while (--jj >= 0) PutMay (kk++, y, c);
y++;
}
} /* PutPixLn */
/*--------------------------------------------------- V_setlin
* Устанавливает атрибуты построения линий:
* размер элементарного пиксела, индекс цвета, кол-во оттенков
* Если размер <= 0, то он не меняется
* Если атрибут цвета < 0, то он не меняется
*/
void V_setlin (sizex, sizey, colorindex, colorvalue)
int sizex, sizey, colorindex;
{
if (sizex > 0) Pix_X= sizex;
if (sizey > 0) Pix_Y= sizey;
if (colorindex >= 0) Pix_C= colorindex;
if (colorvalue >= 0) Pix_V= colorvalue;
} /* V_setlin */
/*----------------------------------------------------- V_DDA
* void V_DDA (int xn, int yn, int xk, int yk)
*
* Подпрограмма построения вектора из точки (xn,yn)
* в точку (xk, yk) в первом квадранте методом
* несимметричного цифрового дифференциального анализатора
* с использованием только целочисленной арифметики.
*
* Обобщение на другие квадранты труда не составляет.
*
* Построение ведется от точки с меньшими координатами
* к точке с большими координатами с единичным шагом по
* координате с большим приращением.
*
* Отдельно выделяется случай вектора с dx == dy
*
* Всего надо выдать пикселы в dx= xk - xn + 1 позиции
* по оси X и в dy= yk - yn + 1 позиции по оси Y.
*
* Для определенности рассмотрим случай dx > dy
*
* При приращении X-координаты на 1 Y-координата должна
* увеличиться на величину меньшую единицы и равную dy/dx.
*
* После того как Y-приращение станет больше или равно 1.0,
* то Y-координату пиксела надо увеличить на 1, а из
* накопленного приращения вычесть 1.0 и продолжить построения
* Т.е. приращение Y на 1 выполняется при условии:
* dy/dx + dy/dx + ... + dy/dx >= 1.0
* Т.к. вычисления в целочисленной арифметике быстрее, то
* умножим на dx обе части и получим эквивалентное условие:
* dy + dy + ... + dy >= dx
*
* Эта схема и реализована в подпрограмме.
*
* При реализации на ассемблере можно избавиться от
* большинства операторов внутри цикла while.
* Для этого перед циклом надо домножить dy на величину,
* равную 65536/dx.
* Тогда надо увеличивать Y на 1 при признаке переноса
* после вычисления s, т.е. операторы
* s= s + dy;
* if (s >= dx) { s= s - dx; yn= yn + 1; }
* заменяются командами ADD и ADC
*
*/
void V_DDA (xn, yn, xk, yk)
int xn, yn, xk, yk;
{ int dx, dy, s;
/* Упорядочивание координат и вычисление приращений */
if (xn > xk) {
s= xn; xn= xk; xk= s;
s= yn; yn= yk; yk= s;
}
dx= xk - xn; dy= yk - yn;
/* Занесение начальной точки вектора */
PutPixLn (xn, yn, Pix_C);
if (dx==0 && dy==0) return;
/* Вычисление количества позиций по X и Y */
dx= dx + 1; dy= dy + 1;
/* Собственно генерация вектора */
if (dy == dx) { /* Наклон == 45 градусов */
while (xn < xk) {
xn= xn + 1;
PutPixLn (xn, xn, Pix_C);
}
} else if (dx > dy) { /* Наклон < 45 градусов */
s= 0;
while (xn < xk) {
xn= xn + 1;
s= s + dy;
if (s >= dx) { s= s - dx; yn= yn + 1; }
PutPixLn (xn, yn, Pix_C);
}
} else { /* Наклон > 45 градусов */
s= 0;
while (yn < yk) {
yn= yn + 1;
s= s + dx;
if (s >= dy) { s= s - dy; xn= xn + 1; }
PutPixLn (xn, yn, Pix_C);
}
}
} /* V_DDA */
/*----------------------------------------------------- V_Bre
* void V_Bre (int xn, int yn, int xk, int yk)
*
* Подпрограмма иллюстрирующая построение вектора из точки
* (xn,yn) в точку (xk, yk) методом Брезенхема.
*
* Построение ведется от точки с меньшими координатами
* к точке с большими координатами с единичным шагом по
* координате с большим приращением.
*
* В общем случае исходный вектор проходит не через вершины
* растровой сетки, а пересекает ее стороны.
* Пусть приращение по X больше приращения по Y и оба они > 0.
* Для очередного значения X нужно выбрать одну двух ближайших
* координат сетки по Y.
* Для этого проверяется как проходит исходный вектор - выше
* или ниже середины расстояния между ближайшими значениями Y.
* Если выше середины, то Y-координату надо увеличить на 1,
* иначе оставить прежней.
* Для этой проверки анализируется знак переменной s,
* соответствующей разности между истинным положением и
* серединой расстояния между ближайшими Y-узлами сетки.
*/
void V_Bre (xn, yn, xk, yk)
int xn, yn, xk, yk;
{ int dx, dy, s, sx, sy, kl, swap, incr1, incr2;
/* Вычисление приращений и шагов */
sx= 0;
if ((dx= xk-xn) < 0) {dx= -dx; --sx;} else if (dx>0) ++sx;
sy= 0;
if ((dy= yk-yn) < 0) {dy= -dy; --sy;} else if (dy>0) ++sy;
/* Учет наклона */
swap= 0;
if ((kl= dx) < (s= dy)) {
dx= s; dy= kl; kl= s; ++swap;
}
s= (incr1= 2*dy)-dx; /* incr1 - констан. перевычисления */
/* разности если текущее s < 0 и */
/* s - начальное значение разности */
incr2= 2*dx; /* Константа для перевычисления */
/* разности если текущее s >= 0 */
PutPixLn (xn,yn,Pix_C); /* Первый пиксел вектора */
while (--kl >= 0) {
if (s >= 0) {
if (swap) xn+= sx; else yn+= sy;
s-= incr2;
}
if (swap) yn+= sy; else xn+= sx;
s+= incr1;
PutPixLn (xn,yn,Pix_C); /* Текущая точка вектора */
}
} /* V_Bre */
/*----------------------------------------------------- V_BreM
* void V_BreM (int xn, int yn, int xk, int yk)
*
* Подпрограмма иллюстрирующая построение ребра залитого
* многоугольника из точки (xn,yn) в точку (xk,yk)
* модифициpованным методом Брезенхема.
*
* Строки многоугольника от занесенного пиксела границы до xk
* заполняются оттенком с максимальным номером.
*/
void V_BreM (xn, yn, xk, yk)
int xn, yn, xk, yk;
{ int dx, dy, sx, sy, kl, swap;
long incr1, incr2;
long s; /* Текущее значение ошибки */
long s_max; /* Макс значение ошибки */
int color_tek; /* Текущий номеp оттенка */
int xt;
/* Вычисление приращений и шагов */
sx= 0;
if ((dx= xk-xn) < 0) {dx= -dx; --sx;} else if (dx>0) ++sx;
sy= 0;
if ((dy= yk-yn) < 0) {dy= -dy; --sy;} else if (dy>0) ++sy;
/* Учет наклона */
swap= 0;
if ((kl= dx) < (s= dy)) {dx= s; dy= kl; kl= s; ++swap;}
s= (long)dx*(long)Pix_V; /* Hачальное значение ошибки */
incr1= 2l*(long)dy /* Конст. перевычисления ошибки */
*(long)Pix_V; /* если текущее s < s_max */
incr2= 2l*s; /* Конст. перевычисления ошибки */
/* если текущее s >= s_max */
s_max= incr2 - incr1; /* Максимальное значение ошибки */
color_tek= Pix_V; /* Яpкость стаpтового пиксела */
if (dx)color_tek=(int)((((long)Pix_V*(long)dy)/(long)dx)/2l);
PutPixLn (xn, yn, Pix_C+color_tek); /* 1-й пиксел */
while (--kl >= 0) {
if (s >= s_max) {
if (swap) xn+= sx; else yn+= sy;
s-= incr2;
}
if (swap) yn+= sy; else xn+= sx;
s+= incr1;
color_tek= Pix_V;
if (dx) color_tek= s / dx /2;
PutPixLn (xn,yn,Pix_C+color_tek); /* Тек.пиксел */
/* Однотонная закраска строки многоугольника макс цветом */
xt= xn;
while (++xt <= xk) PutPixLn (xt,yn,Pix_C+Pix_V-1);
}
} /* V_BreM */
/*================================================= T_VECTOR.C
* ТЕСТ ГЕНЕРАЦИИ ВЕКТОРОВ
*
* Строит вектора из точки Xn,Yn в заданную
* Программа запрашивает ввод четыpех чисел:
* mode = -2 - прекращение работы
* -1 - очистка экрана
* 0 - вывод сетки
* 1-7 построение вектоpа:
* 1рр == 1 - по алгоритму ЦДА
* 2рр == 1 - по алгоритму Брезенхема
* 3рр == 1 - по модифиц. алгоритму Брезенхема
* иное значение - замена Xn,Yn на введенные Xk,Yk
* atrib - атpибуты постpоения в виде десятичного числа
* из 8 цифр - PPСCCVVV:
* PP - pазмеp элементаpного пиксела
* ССС - начальный номер оттенка
* VVV - количество оттенков
* Xk - конечная координата вектора
* Yk
*/
#include "V_VECTOR.C"
#define MODE_256 1 /* 0/1 - обычный VGA/SVGA режим */
#if MODE_256
# include "V_SVGA.C"
#endif
#include <conio.h>
#include <graphics.h>
#include <stdio.h>
#include <stdlib.h>
/*------------------------------------------------------- Grid
* Строит сетку 10*10
*/
void Grid (int col)
{ int Xn,Yn,Xk,Yk;
setcolor (col);
Xn= 0; Xk= getmaxx();
Yn= 0; Yk= getmaxy();
while (Xn <= Xk) {line (Xn,Yn,Xn,Yk); Xn+= 10; }
Xn= 0;
while (Yn <= Yk) {line (Xn,Yn,Xk,Yn); Yn+= 10; }
} /* Grid */
/*----------------------------------------- MAIN T_VECTOR.C */
void main (void)
{
int ii, jj,
mode=1, /* Режим pаботы */
Xn=0,Yn=0, /* Координаты начала отрезка */
Xk,Yk, /* Координаты конца отрезка */
fon, /* Индекс цвета фона */
col_beg, col_val, /* Атpибуты пикселов */
xpix, ypix,
colgrid, /* Цвет сетки */
col_lin= 200, /* Цвет "точного" отрезка */
col_Bre= 201, /* Цвет построения для ЦДА */
col_DDA= 202; /* Цвет построения для Брезенхема */
int gdriver= DETECT, gmode;
long atrib=5064064l,la;/* Размеp пиксела*100+цвета */
#if MODE_256
V_ini256 (&gdriver, &gmode, "");
jj= getmaxcolor();
for (ii=0; ii<=jj; ++ii) /* Ч/б палитра */
setrgbpalette (ii, ii, ii, ii);
atrib=5064064l; /* Пиксел 5х5, нач цвет=64*/
colgrid= 170; /* Цвет сетки */
fon= 140;
setrgbpalette(7,255,255,255);/* Цвет для printf */
#else
initgraph (&gdriver, &gmode, "");
atrib= 5000016l; /* Пиксел 5х5, нач цвет=0*/
colgrid= 9;
fon= 8;
#endif
setbkcolor(fon); /* Очистка экрана */
cleardevice();
Xk= getmaxx(); Yk= getmaxy();
Grid (colgrid);
/* Цвет для построения алгоритмом ЦДА */
setrgbpalette(col_lin,63, 0,0); /* Цвет точного отрезка */
setrgbpalette(col_DDA,63,63,0); /* Цвет для ЦДА */
setrgbpalette(col_Bre,00,63,0); /* Цвет для Брезенхема */
for (;;) {
gotoxy (1, 1);
printf(" ");
printf(" \r");
printf("mode atrib Xk Yk= (%d %ld %d %d) ? ",
mode, atrib, Xk, Yk);
scanf ("%d%ld%d%d", &mode, &atrib, &Xk, &Yk);
xpix= ypix= atrib / 1000000l;
la= atrib % 1000000l;
col_beg= la / 1000l;
col_val= la % 1000l;
if (mode == -2) goto konec; else
if (mode == -1) cleardevice(); else
if (!mode) Grid (colgrid); else
if (mode & 7) {
if (mode & 1) {
V_setlin (xpix, ypix, col_DDA, 1);
V_DDA (Xn, Yn, Xk, Yk);
/* Постpоение "точного" отpезка */
setcolor (col_lin);
line (Xn, Yn, Xk*xpix, Yk*ypix);
}
if (mode & 2) {
V_setlin (xpix, ypix, col_Bre, 1);
V_Bre (Xn, Yn+3, Xk, Yk+3);
/* Постpоение "точного" отpезка */
setcolor (col_lin);
line (Xn, (Yn+3)*ypix, Xk*xpix, (Yk+3)*ypix);
}
if (mode & 4) {
V_setlin (xpix, ypix, col_beg, col_val);
V_BreM (Xn, Yn+6, Xk, Yk+6);
/* Постpоение "точного" отpезка */
setcolor (col_lin);
line (Xn, (Yn+6)*ypix, Xk*xpix, (Yk+6)*ypix);
}
} else {
Xn= Xk; Yn= Yk;
}
}
konec:
closegraph();
} /* main */
В данном приложении содержатся процедуры поддержки низкочастотной фильтрации растровых изображений и процедуры усреднения растровых изображений с понижением разрешения, а также тестовая программа демонстрирующая их работу.
Всего представлены две процедуры низкочастотной фильтрации V_fltr0 и V_fltr1, предназначенные для обработки изображений прямо в видеопамяти и с построчной буферизацией в оперативной памяти, соответственно. Последняя при модификации вспомогательных процедур доступа к изображению может обрабатывать картины, находящиеся в файле на внешнем носителе или просто в оперативной памяти.
Аналогично, представлены две процедуры усреднения изображения с понижением разрешения - V_fltr2 и V_fltr3.
При фильтрации и усреднении может использоваться одна из пяти предусмотренных масок фильтрации.
/*================================================== V_FILTR.C
* В файле V_FILTR.C содержатся процедуры
* поддержки фильтрации изображений:
*
* GetStr, PutStr - служебные
*
* V_fltr0 - фильтрует изображение в прямоугольной области,
* работая прямо с видеопамятью
* V_fltr1 - фильтрует изображение в прямоугольной области,
* работая с буферами строк
* V_fltr2 - усредняет картину по маске с понижением
* разрешения, работая прямо с видеопамятью
* V_fltr3 - усредняет картину по маске с понижением
* разрешения, работая с буферами строк
*/
#include <alloc.h>
#define GetMay getpixel
#define PutMay putpixel
static int
Mask0[]= {1,1, 1,1 },
Mask1[]= {1,1,1, 1,1,1, 1,1,1 },
Mask2[]= {1,1,1, 1,2,1, 1,1,1 },
Mask3[]= {1,2,1, 2,4,2, 1,2,1 },
Mask4[]= {1,1,1,1,
1,1,1,1,
1,1,1,1,
1,1,1,1 },
Mask5[]= {1,2, 3, 4, 3,2,1,
2,4, 6, 8, 6,4,2,
3,6, 9,12, 9,6,5,
4,8,12,16,12,8,4,
3,6, 9,12, 9,6,5,
2,4, 6, 8, 6,4,2,
1,2, 3, 4, 3,2,1 },
Mask_ln[]= {2, 3, 3, 3, 4, 7}, /* Размер маски */
Mask_st[]= {2, 2, 2, 2, 4, 4}, /* Шаг усреднения */
Mask_vl[]= {4, 9,10,16,16,256}, /* Сумма элементов */
*Mask_bg[]={ /* Адреса начал */
Mask0,Mask1,Mask2,Mask3,Mask4,Mask5
};
/*----------------------------------------------------- GetStr
* Запрашивает фрагмент растровой строки из видеопамяти
*/
static void GetStr (st, Yst, Xn, Xk)
char *st; int Yst, Xn, Xk;
{ while (Xn <= Xk) *st++= GetMay (Xn++, Yst); }
/*----------------------------------------------------- PutStr
* Записывает фрагмент растровой строки в видеопамять
*/
static void PutStr (st, Yst, Xn, Xk)
char *st; int Yst, Xn, Xk;
{while (Xn <= Xk) PutMay (Xn++, Yst, *st++); }
/*---------------------------------------------------- V_fltr0
* Фильтрует изображение в прямоугольной области,
* работая прямо с видеопамятью
* msknum = 0-5 - номер маски фильтра
* Xn_source,Yn_source - окно исходного изображения
* Xk_source,Xk_source
* Xn_target,Yn_target - верхний левый угол результата
*/
void V_fltr0 (msknum,Xn_source,Yn_source,Xk_source,Yk_source,
Xn_target,Yn_target)
int msknum,Xn_source,Yn_source,Xk_source,Yk_source,
Xn_target,Yn_target;
{
char *plut; /* Указатель палитры */
int *pi; /* Тек указат маски */
int pixel; /* Пиксел исх изображения */
int *Maska, /* Указатель маски */
Mask_Y,Mask_X, /* Размеры маски */
X_centr,Y_centr,/* Центр маски */
Mask_sum, /* Сумма элементов */
Xk, /* Предельные положения маски */
Yk, /* в исходной области */
s, sr, sg, sb, /* Скаляры для суммир в маской */
ii, jj,
Xt, Yt;
/* Запрос параметров маски */
Maska= Mask_bg[msknum]; /* Указатель маски */
Mask_Y= Mask_X= Mask_ln[msknum]; /* Размеры маски */
X_centr= Mask_X / 2; /* Центр маски */
Y_centr= Mask_Y / 2;
Mask_sum= Mask_vl[msknum]; /* Сумма элементов */
/* Предельные положения маски в исходной области */
Xk= Xk_source+1-Mask_X;
Yk= Yk_source+1-Mask_Y;
/*------- Фильтрация с прямой работой с видеопамятью -------*/
for (Yt= Yn_source; Yt<=Yk; ++Yt) {
for (Xt=Xn_source; Xt<=Xk; ++Xt) {
pi= Maska; sr=0; sg=0; sb=0; /* Суммированные RGB*/
for (ii=0; ii<Mask_Y; ++ii)
for (jj=0; jj<Mask_X; ++jj) {
pixel= GetMay (Xt+jj, Yt+ii);
plut= &V_pal256[pixel][0];
s= *pi++; /* Элемент маски */
sr+= (s * *plut++); /* Суммирование */
sg+= (s * *plut++); /* по цветам с */
sb+= (s * *plut++); /* весами маски */
}
sr /= Mask_sum; sg /= Mask_sum; sb /= Mask_sum;
/* Поиск элемента ТЦ, наиболее подходящего для данных R,G,B */
ii= V_clrint (sr, sg, sb);
PutMay (Xn_target+(Xt-Xn_source)+X_centr,
Yn_target+(Yt-Yn_source)+Y_centr, ii);
}
}
} /* V_fltr0 */
/*---------------------------------------------------- V_fltr1
* Фильтрует изображение в прямоугольной области,
* работая с буферами строк
* msknum = 0-5 - номер маски фильтра
* Xn_source,Yn_source - окно исходного изображения
* Xk_source,Xk_source
* Xn_target,Yn_target - верхний левый угол результата
*/
void V_fltr1 (msknum,Xn_source,Yn_source,Xk_source,Yk_source,
Xn_target,Yn_target)
int msknum,Xn_source,Yn_source,Xk_source,Yk_source,
Xn_target,Yn_target;
{
char *plut; /* Указатель палитры */
int *pi; /* Тек указат маски */
int pixel; /* Пиксел исх изображения */
int *Maska, /* Указатель маски */
Mask_Y,Mask_X, /* Размеры маски */
X_centr,Y_centr,/* Центр маски */
Mask_sum, /* Сумма элементов */
Xk, /* Предельные положения маски */
Yk, /* в исходной области */
Dx_source, /* Размер строки исх изображения */
Ystr, /* Y тек читаемой строки изображ */
s, sr, sg, sb, /* Скаляры для суммир в маской */
ii, jj,
Xt, Yt;
char *ps, *sbuf, *pt, *tbuf, *ptstr[8];
Dx_source= Xk_source-Xn_source+1;
/* Запрос параметров маски */
Maska= Mask_bg[msknum]; /* Указатель маски */
Mask_Y= Mask_X= Mask_ln[msknum]; /* Размеры маски */
X_centr= Mask_X / 2; /* Центр маски */
Y_centr= Mask_Y / 2;
Mask_sum= Mask_vl[msknum]; /* Сумма элементов */
/* Предельные положения маски в исходной области */
Xk= Xk_source+1-Mask_X;
Yk= Yk_source+1-Mask_Y;
/* Заказ буферов */
if ((sbuf= malloc (Dx_source * Mask_Y)) == NULL) goto all;
if ((tbuf= malloc (Dx_source)) == NULL)
goto fr_sbuf;
/*------- Фильтрация с использованием буферов строк --------*/
/* Подготовка массива указателей на строки
* ptstr[0] --> последняя строка
* ptstr[1] --> строка 0
* ptstr[2] --> строка 1
* и т.д.
*/
ps= sbuf; ii= Mask_Y; jj= 1;
do {
ptstr[jj]= ps; ps+= Dx_source;
if (++jj == Mask_Y) jj= 0;
} while (--ii > 0);
/* Начальное чтение Mask_Y - 1 строк */
Ystr= Yn_source;
for (ii=1; ii<Mask_Y; ++ii)
GetStr (ptstr[ii], Ystr++, Xn_source, Xk_source);
for (Yt= Yn_source; Yt<=Yk; ++Yt) {
/* Запрос следующей строки и циклический сдвиг указателей */
GetStr (ps= ptstr[0], Ystr++, Xn_source, Xk_source);
jj= Mask_Y-1;
for (ii=0; ii<jj; ++ii) ptstr[ii]= ptstr[ii+1];
ptstr[jj]= ps;
pt= tbuf;
for (Xt=Xn_source; Xt<=Xk; ++Xt) {
pi= Maska; sr=0; sg=0; sb=0; /* Суммированные RGB*/
for (ii=0; ii<Mask_Y; ++ii) {
ps= ptstr[ii] + (Xt-Xn_source);
for (jj=0; jj<Mask_X; ++jj) {
plut= &V_pal256[*ps++ & 255][0];
s= *pi++; /* Элемент маски */
sr+= (s * *plut++); /* Суммирование */
sg+= (s * *plut++); /* по цветам с */
sb+= (s * *plut++); /* весами маски */
}
}
sr /= Mask_sum; sg /= Mask_sum; sb /= Mask_sum;
/* Поиск элемента ТЦ, наиболее подходящего для данных R,G,B */
*pt++= V_clrint (sr, sg, sb);
}
PutStr (tbuf, /* Запись строки */
Yn_target + Y_centr + (Yt-Yn_source) ,
Xn_target + X_centr,
Xn_target + X_centr + (--pt - tbuf));
}
free (tbuf);
fr_sbuf:
free (sbuf);
all:;
} /* V_fltr1 */
/*---------------------------------------------------- V_fltr2
* Усредняет картину по маске с понижением разрешения,
* работая прямо с видеопамятью
* msknum = 0-5 - номер маски фильтра
* Xn_source,Yn_source - окно исходного изображения
* Xk_source,Xk_source
* Xn_target,Yn_target - верхний левый угол результата
*/
void V_fltr2 (msknum,Xn_source,Yn_source,Xk_source,Yk_source,
Xn_target,Yn_target)
int msknum,Xn_source,Yn_source,Xk_source,Yk_source,
Xn_target,Yn_target;
{
char *plut; /* Указатель палитры */
int *pi; /* Тек указат маски */
int pixel; /* Пиксел исх изображения */
int *Maska, /* Указатель маски */
Mask_Y,Mask_X, /* Размеры маски */
X_centr,Y_centr,/* Центр маски */
Mask_sum, /* Сумма элементов */
Xk, /* Предельные положения маски */
Yk, /* в исходной области */
s, sr, sg, sb, /* Скаляры для суммир в маской */
Xr,Yr, /* Координаты пиксела результата */
Sm, /* Сдвиг маски для обраб след точки */
ii, jj,
Xt, Yt;
/* Запрос параметров маски */
Maska= Mask_bg[msknum]; /* Указатель маски */
Mask_Y= Mask_X= Mask_ln[msknum]; /* Размеры маски */
X_centr= Mask_X / 2; /* Центр маски */
Y_centr= Mask_Y / 2;
Mask_sum= Mask_vl[msknum]; /* Сумма элементов */
/* Предельные положения маски в исходной области */
Xk= Xk_source+1-Mask_X;
Yk= Yk_source+1-Mask_Y;
Yt= Yn_source;
Yr= Yn_target+Y_centr;
Sm= Mask_st[msknum]; /* Шаг усреднения*/
while (Yt <= Yk) {
Xt=Xn_source; Xr= Xn_target+X_centr;
while (Xt <= Xk) {
pi= Maska; sr=0; sg=0; sb=0; /* Суммированные RGB*/
for (ii=0; ii<Mask_Y; ++ii)
for (jj=0; jj<Mask_X; ++jj) {
pixel= GetMay (Xt+jj, Yt+ii);
plut= &V_pal256[pixel][0];
s= *pi++; /* Элемент маски */
sr+= (s * *plut++); /* Суммирование */
sg+= (s * *plut++); /* по цветам с */
sb+= (s * *plut++); /* весами маски */
}
sr /= Mask_sum; sg /= Mask_sum; sb /= Mask_sum;
/* Поиск элемента ТЦ, наиболее подходящего для данных R,G,B */
ii= V_clrint (sr, sg, sb);
PutMay (Xr++, Yr, ii);
Xt+= Sm;
}
Yt+= Sm; ++Yr;
}
} /* V_fltr2 */
/*---------------------------------------------------- V_fltr3
* Усредняет картину по маске с понижением разрешения,
* работая с буферами строк
* msknum = 0-5 - номер маски фильтра
* Xn_source,Yn_source - окно исходного изображения
* Xk_source,Xk_source
* Xn_target,Yn_target - верхний левый угол результата
*/
void V_fltr3 (msknum,Xn_source,Yn_source,Xk_source,Yk_source,
Xn_target,Yn_target)
int msknum,Xn_source,Yn_source,Xk_source,Yk_source,
Xn_target,Yn_target;
{
char *plut; /* Указатель палитры */
int *pi; /* Тек указат маски */
int pixel; /* Пиксел исх изображения */
int *Maska, /* Указатель маски */
Mask_Y,Mask_X, /* Размеры маски */
X_centr,Y_centr,/* Центр маски */
Mask_sum, /* Сумма элементов */
Xk, /* Предельные положения маски */
Yk, /* в исходной области */
Dx_source, /* Размер строки исх изображения */
s, sr, sg, sb, /* Скаляры для суммир в маской */
Xr,Yr, /* Координаты пиксела результата */
Sm, /* Сдвиг маски для обраб след точки */
ii, jj,
Xt, Yt;
char *ps, *sbuf, *pt, *tbuf, *ptstr[8];
Dx_source= Xk_source-Xn_source+1;
/* Запрос параметров маски */
Maska= Mask_bg[msknum]; /* Указатель маски */
Mask_Y= Mask_X= Mask_ln[msknum]; /* Размеры маски */
X_centr= Mask_X / 2; /* Центр маски */
Y_centr= Mask_Y / 2;
Mask_sum= Mask_vl[msknum]; /* Сумма элементов */
/* Предельные положения маски в исходной области */
Xk= Xk_source+1-Mask_X;
Yk= Yk_source+1-Mask_Y;
/* Заказ буферов */
if ((sbuf= malloc (Dx_source * Mask_Y)) == NULL) goto all;
if ((tbuf= malloc (Dx_source/Mask_st[msknum]+16)) == NULL)
goto fr_sbuf;
/* Подготовка массива указателей на строки
* ptstr[0] --> строка 0
* ptstr[1] --> строка 1
* ptstr[2] --> строка 2
* и т.д.
*/
ps= sbuf;
for (ii=0; ii<Mask_Y; ++ii) {
ptstr[ii]= ps; ps+= Dx_source;
}
Yt= Yn_source;
Yr= Yn_target+Y_centr;
Sm= Mask_st[msknum]; /* Шаг усреднения*/
while (Yt <= Yk) {
for (ii=0; ii<Mask_Y; ++ii) /* Чтен исх строк */
GetStr (ptstr[ii], Yt+ii, Xn_source, Xk_source);
Xt=Xn_source; pt= tbuf;
while (Xt <= Xk) {
pi= Maska; sr=0; sg=0; sb=0; /* Суммированные RGB*/
for (ii=0; ii<Mask_Y; ++ii) {
ps= ptstr[ii] + (Xt-Xn_source);
for (jj=0; jj<Mask_X; ++jj) {
plut= &V_pal256[*ps++ & 255][0];
s= *pi++; /* Элемент маски */
sr+= (s * *plut++); /* Суммирование */
sg+= (s * *plut++); /* по цветам с */
sb+= (s * *plut++); /* весами маски */
}
}
sr /= Mask_sum; sg /= Mask_sum; sb /= Mask_sum;
/* Поиск элемента ТЦ, наиболее подходящего для данных R,G,B */
*pt++= V_clrint (sr, sg, sb);
Xt+= Sm;
}
PutStr (tbuf,Yr++, /* Запись строки */
Xn_target+X_centr,
Xn_target+X_centr + (--pt - tbuf));
Yt+= Sm;
}
free (tbuf);
fr_sbuf:
free (sbuf);
all:;
} /* V_fltr3 */
/*================================================== T_FILTR.C
*
* ТЕСТ ФИЛЬТРАЦИИ
*
* Программа вначале строит два смещенных вектора
* большими пикселами, затем последовательно для каждой
* из пяти масок:
* - фильтрует с непосредственным доступом к видеопамяти
* - фильтрует с буферизацией растровых строк
* - формирует усредненную картинку меньшего разрешения
* с непосредственным доступом к видеопамяти
* - формирует усредненную картинку меньшего разрешения
* с буферизацией растровых строк
*
* После вывода очередной картинки ждет нажатия любой клавиши
*
* Виды масок:
* 0: 1 1 1: 1 1 1 2: 1 1 1 3: 1 2 1
* 1 1 1 1 1 1 2 1 2 4 2
* 1 1 1 1 1 1 1 2 1
*
* 4: 1 1 1 1 5: 1 2 3 4 3 2 1
* 1 1 1 1 2 4 6 8 6 4 2
* 1 1 1 1 3 6 9 12 9 6 5
* 1 1 1 1 4 8 12 16 12 8 4
* 3 6 9 12 9 6 5
* 2 4 6 8 6 4 2
* 1 2 3 4 3 2 1
*/
#include "V_VECTOR.C"
#include "VGA_256.C"
#include "V_FILTR.C"
#include <conio.h>
#include <graphics.h>
#include <stdio.h>
#define VECTOR 0 /* 0/1 - фикс вектор/ввод координат */
/*------------------------------------------------------- Grid
* Строит сетку 10*10
*/
void Grid (void)
{ int Xn,Yn,Xk,Yk;
setcolor (170);
Xn= 0; Xk= getmaxx();
Yn= 0; Yk= getmaxy();
while (Xn <= Xk) {line (Xn,Yn,Xn,Yk); Xn+= 10; }
Xn= 0;
while (Yn <= Yk) {line (Xn,Yn,Xk,Yn); Yn+= 10; }
} /* Grid */
/*---------------------------------------------- main Filtr */
void main (void)
{
int ii, jj,
mov_lin, /* 0/1 - позиционир/отрезок */
Xn,Yn,Xk,Yk, /* Координаты отрезка */
fon= 140; /* Индекс фона */
int gdriver= DETECT, gmode;
int Xn_source, Yn_source, /* Фильтруемая область */
Xk_source, Yk_source,
Dx_source;
int Xn_target, Yn_target, /* Результаты фильтрации */
Xk_target, Yk_target;
int msknum; /* Номер текущей маски */
char *ps;
V_ini256 (&gdriver, &gmode, "");
ps= (char *)V_pal256;
for (ii=0; ii<=255; ++ii) { /* Ч/б палитра */
jj= ii / 4;
*ps++= jj; *ps++= jj; *ps++= jj;
setrgbpalette (ii, jj, jj, jj);
}
setbkcolor(fon); /* Очистка экрана */
cleardevice();
Xk= getmaxx(); Yk= getmaxy();
/* Начальные установки для фильтрации */
Xn_source= 0; /* Исходная область */
Yn_source= 0;
Xk_source= (Xk + 1)/2 - 1;
Yk_source= Yk;
Xn_target= Xk_source + 1; /* Результ. область */
Yn_target= 0;
Xk_target= Xk;
Yk_target= Yk_source;
Dx_source= Xk_source-Xn_source+1; /* X-размер исходной*/
#if VECTOR
Grid ();
mov_lin= 1; Xn= 0; Yn= 0; Xk= 0; Yk= 0;
for (;;) {
gotoxy (1, 1);
printf(" \r");
printf("mov_lin Xk Yk= (%d %d %d) ? ", mov_lin, Xk, Yk);
scanf ("%d%d%d", &mov_lin, &Xk, &Yk);
if (mov_lin < 0) cleardevice(); else
if (!mov_lin) Grid (); else {
if (mov_lin & 1) V_DDA (0, 0, Xk, Yk);
if (mov_lin & 2) V_Bre (0, 0, Xk, Yk);
}
}
#else
Xk= Dx_source / Pix_X - 1;
Yk= (Yk_source-Yn_source+1) / Pix_Y - 1;
V_DDA (Xn_source, Yn_source, Xk, Yk-17);
V_Bre (Xn_source, Yn_source+17, Xk, Yk);
getch();
#endif
ii= 0xF; /* Обе фильтрации и оба сжатия */
setfillstyle (SOLID_FILL, fon);
for (msknum=0; msknum<6; ++msknum) {
if (ii & 1) { /* Фильтрация из видеоозу */
bar (Xn_target, Yn_target, Xk_target, Yk_target);
V_fltr0 (msknum,Xn_source,Yn_source,
Xk_source,Yk_source,Xn_target,Yn_target);
getch ();
}
if (ii & 2) { /* Фильтрация из буферов */
bar (Xn_target, Yn_target, Xk_target, Yk_target);
V_fltr1 (msknum,Xn_source,Yn_source,
Xk_source,Yk_source,Xn_target,Yn_target);
getch ();
}
if (ii & 4) { /* Сжатие из из видеоозу */
bar (Xn_target, Yn_target, Xk_target, Yk_target);
V_fltr2 (msknum,Xn_source,Yn_source,
Xk_source,Yk_source,Xn_target,Yn_target);
getch ();
}
if (ii & 8) { /* Сжатие из буферов */
bar (Xn_target, Yn_target, Xk_target, Yk_target);
V_fltr3 (msknum,Xn_source,Yn_source,
Xk_source,Yk_source,Xn_target,Yn_target);
getch ();
}
}
closegraph();
} /* main */
В данном приложении помещены процедуры генерации окружностей по алгоритму Брезенхема и Мичнера, а также программа T_Circle для тестирования данных процедур.
/*--------------------------------------------------- V_Circle
* Подпрограммы для генерации окружности
* Pixel_circle - занесение пикселов с учетом симметрии
* V_BRcirc - генерирует окружность по алгоритму
* Брезенхема.
* V_MIcirc - генерирует окружность по алгоритму
* Мичнера.
*/
#include <graphics.h>
/*----------------------------------------------- Pixel_circle
* Заносит пикселы окружности по часовой стрелке
*/
static void Pixel_circle (xc, yc, x, y, pixel)
int xc, yc, x, y, pixel;
{
putpixel(xc+x, yc+y, pixel);
putpixel(xc+y, yc+x, pixel);
putpixel(xc+y, yc-x, pixel);
putpixel(xc+x, yc-y, pixel);
putpixel(xc-x, yc-y, pixel);
putpixel(xc-y, yc-x, pixel);
putpixel(xc-y, yc+x, pixel);
putpixel(xc-x, yc+y, pixel);
} /* Pixel_circle */
/*--------------------------------------------------- V_BRcirc
* Генерирует 1/8 окружности по алгоритму Брезенхема
*
* Процедура может строить 1/4 окружности.
* Для этого надо цикл while заменить на for (;;)
* и после Pixel_circle проверять достижение конца по условию
* if (y <= end) break;
* Где end устанавливается равным 0
* В этом случае не нужен и последний оператор
* if (x == y) Pixel_circle (xc, yc, x, y, pixel);
* Генерацию 1/8 можно обеспечить задав end = r / sqrt (2)
*/
void V_BRcirc (xc, yc, r, pixel)
int xc, yc, r, pixel;
{ int x, y, z, Dd;
x= 0; y= r; Dd= 2*(1-r);
while (x < y) {
Pixel_circle (xc, yc, x, y, pixel);
if (!Dd) goto Pd;
z= 2*Dd - 1;
if (Dd > 0) {
if (z + 2*x <= 0) goto Pd; else goto Pv;
}
if (z + 2*y > 0) goto Pd;
Pg: ++x; Dd= Dd + 2*x + 1; continue; /* Горизонт */
Pd: ++x; --y; Dd= Dd + 2*(x-y+1); continue; /* Диагонал */
Pv: --y; Dd= Dd - 2*y + 1; /* Вертикал */
}
if (x == y) Pixel_circle (xc, yc, x, y, pixel);
} /* V_BRcirc */
/*--------------------------------------------------- V_MIcirc
* Генерирует 1/8 окружности по алгоритму Мичнера
*/
void V_MIcirc (xc, yc, r, pixel)
int xc, yc, r, pixel;
{ int x, y, d;
x= 0; y= r; d= 3 - 2*r;
while (x < y) {
Pixel_circle (xc, yc, x, y, pixel);
if (d < 0) d= d + 4*x + 6; else {
d= d + 4*(x-y) + 10; --y;
}
++x;
}
if (x == y) Pixel_circle (xc, yc, x, y, pixel);
} /* V_MIcirc */
/*=============================================== T_CIRCLE.C
*
* ТЕСТ ГЕНЕРАЦИИ ОКРУЖНОСТЕЙ
*
* Запрашивает ввод четырех чисел - координат центра,
* радиуса и цвета построения: Xc Yc R Pix
*
* Затем строит заданную окружность по алгоритму Брезенхема
* и концентрично с ней с радиусом, уменьшенным на 2, и
* номером цвета, уменьшенным на 1, выдает окружность по
* алгоритму Мичнера.
*
* При вводе Xc < 0 программа прекращает работу
*/
#include <graphics.h>
#include <stdio.h>
#include "V_CIRCLE.C"
/*-------------------------------------------- MAIN T_CIRCLE.C
*/
void main (void)
{
int ii, Xc=300, Yc=240, R=238, Pix=14;
int gdriver = DETECT, gmode;
initgraph(&gdriver, &gmode, "c:\tc\bgi");
if ((ii= graphresult()) != grOk) {
printf ("Err=%d\n", ii); goto all;
}
setbkcolor(0);
cleardevice();
for (;;) {
gotoxy (1,1);
printf(" \r");
printf("Xc, Yc, R, Pix= (%d %d %d %d) ? ", Xc,Yc,R,Pix);
scanf ("%d%d%d%d", &Xc, &Yc, &R, &Pix);
if (Xc < 0) break;
V_BRcirc (Xc, Yc, R, Pix);
V_MIcirc (Xc, Yc, R-2, Pix-1);
}
all:
closegraph();
}
В данном приложении приведены две процедуры заливки многоугольника: V_FP0 и V_FP1. Обе они реализуют алгоритм построчного заполнения, описанный в разделе 5.
В данных процедурах все массивы используются, начиная с элемента с индексом 1, а не 0, как это принято в языке C.
/*===================================================== V_FP0
* Простая (и не слишком эффективная) подпрограмма
* однотонной заливки многоугольника методом построчного
* сканирования. Имеет место дублирование закраски
* строк.
* Более эффективная программа, практически не дублирующая
* занесение пикселов, - V_FP1 приведена далее в этом
* приложении.
*/
#include <stdio.h>
#include <graphics.h>
#define MAXARR 300 /* Макс кол-во вершин многоугольника */
#define MAXLST 300 /* Макс размер списка активных ребер */
/*---------------------------------------------------- FILSTR
* Заливает строку iy от ixn до ixk
*
* void FILSTR (int kod, int iy, int ixn, int ixk)
*/
void FILSTR (kod, iy, ixn, ixk)
int kod, iy, ixn, ixk;
{
while (ixn <= ixk) putpixel (ixn++, iy, kod);
} /* FILSTR */
/*---------------------------------------------------- SORT
* Сортирует n элементов iarr по возрастанию
*/
void SORT (n, iarr)
int n, *iarr;
{ int ii, jj, kk, ll, min;
for (ii=0; ii<n; ++ii) {
min= iarr[ll= ii];
for (jj=ii+1; jj<n; ++jj)
if ((kk= iarr[jj]) < min) {ll= jj; min= kk; }
if (ll != ii) {iarr[ll]= iarr[ii]; iarr[ii]= min; }
}
} /* SORT */
/*--------------- Глобалы процедуры закраски ---------------*/
static int KOD, NWER; /* Код заливки и количество вершин */
static float *pt_X; /* Массивы входных координат вершин */
static float *pt_Y;
static int ntek; /* Номер текущей вершины */
/* Список активных ребер */
static int idlspi; /* Длина списка активных ребер */
static int IYREB[MAXLST]; /* Макс Y-коорд активных ребер */
static float RXREB[MAXLST]; /* Тек X-коорд активных ребер */
static float RPRIR[MAXLST]; /* X-приращение на 1 шаг по Y */
/*---------------------------------------------------- OBRREB
* По данным :
* NWER - количество вершин,
* ntek - номер текущей вершины,
* isd = -1/+1 - сдвиг для вычисления номера
* соседней вершины - слева/справа
* вычисляет DY,
* Если DY < 0 то вершина уже обработана,
* Если DY == 0 то вершины на одном Y, т.е.
* строится горизонтальный отрезок,
* Если DY > 0 то формируется новый элемент списка
* активных ребер
*/
static void OBRREB (isd)
int isd;
{
int inext,iyt,ixt;
float xt, xnext, dy;
inext= ntek + isd;
if (inext < 1) inext= NWER;
if (inext > NWER) inext= 1;
dy= pt_Y[inext] - pt_Y[ntek];
if (dy < 0) goto RETOBR;
xnext= pt_X[inext];
xt= pt_X[ntek];
if (dy != 0) goto DYNE0;
iyt= pt_Y[ntek];
inext= xnext;
ixt= xt;
FILSTR (KOD, iyt, inext, ixt);
goto RETOBR;
DYNE0:
idlspi++;
IYREB[idlspi]= pt_Y[inext];
RXREB[idlspi]= xt;
RPRIR[idlspi]= (xnext - xt) / dy;
RETOBR:;
} /* OBRREB */
/*---------------------------------------------------- V_FP0
* Однотонно заливает многоугольник,
* заданный координатами вершин
*
* void V_FP0 (int pixel, int kol, float *Px, float *Py)
*
*/
void V_FP0 (pixel, kol, Px, Py)
int pixel, kol; float *Px, *Py;
{
int ii, jj, kk;
int iymin; /* Мин Y-координата многоугольн */
int iymax; /* Макс Y-координата многоугольн */
int iysled; /* Y-коорд появления новых вершин */
int iytek;
int ikledg; /* Кол-во вершин с данным iytek */
int ibgind; /* Нач индекс таких вершин */
int iedg[MAXARR]; /* Y-коорд вершин по возрастанию */
int inom[MAXARR]; /* Их номера в исходном массиве Py */
int irabx[MAXLST]; /* X-коорд пересечений в строке сканир */
KOD= pixel; /* Параметры в глобалы */
NWER= kol;
pt_X= Px;
pt_Y= Py;
/* Построение массивов Y и их номеров */
for (ii=1; ii<=kol; ++ii) {
iedg[ii]= Py[ii]; inom[ii]= ii;
}
/* Cовместная сортировка Y-коорд вершин и их номеров */
for (ii=1; ii <= kol; ++ii) {
iymin= iedg[ii];
ntek= ii;
for (jj=ii+1; jj <= kol; ++jj)
if (iedg[jj] < iymin) {iymin= iedg[jj]; ntek= jj; }
if (ntek != ii) {
iedg[ntek]= iedg[ii]; iedg[ii]= iymin;
iymin= inom[ntek];
inom[ntek]= inom[ii]; inom[ii]= iymin;
}
}
idlspi= 0; /* Начальные присвоения */
ibgind= 1;
iytek= iedg[1];
iymax= iedg[kol];
/* Цикл раскраски */
/* ikledg = кол-во вершин с данным iytek
* ibgind = индексы таковых в массиве inom
*/
FORM_EDGES:
ikledg= 0;
for (ii=ibgind; ii<=kol; ++ii)
if (iedg[ii] != iytek) break; else ikledg++;
/* Цикл построения списка активных ребер
* и закрашивание горизонтальных ребер
*/
/* Построение списка активных ребер (САР) */
for (ii=1; ii<=ikledg; ++ii) {
ntek= inom[ ibgind+ii-1]; /* Исх ном тек вершины */
OBRREB (-1); /* DY с соседями затем */
OBRREB (+1); /* либо отказ, либо */
/* горизонталь, либо */
} /* измен списка активных*/
if (!idlspi) goto KOHGFA;
ii= ibgind + ikledg; /* Y ближайшей вершины */
iysled= iymax;
if (ii < kol) iysled= iedg[ii];
/* Горизонтальная раскраска по списку */
for (ii=iytek; ii<=iysled; ++ii) {
/* Выборка X-ов из списка активных ребер (САР) */
for (jj=1; jj <= idlspi; ++jj)
irabx[jj]= RXREB[jj];
SORT (idlspi, irabx+1); /* Сортировка X-ов */
for (jj=1; jj<=idlspi-1; jj+= 2) /* Заливка */
FILSTR (pixel, ii, irabx[jj], irabx[jj+1]);
if (ii == iysled) continue;
for (jj=1; jj <= idlspi; ++jj) /* Перестройка САР */
RXREB[jj]= RXREB[jj] + RPRIR[jj];
}
if (iysled == iymax) goto KOHGFA;
/* Выбрасывание из списка всех ребер с YMAK ребра = YSLED */
ii= 0;
M1:ii++;
M2:if (ii > idlspi) goto WYBROSILI;
if (IYREB[ii] != iysled) goto M1;
--idlspi;
for (jj=ii; jj <= idlspi; ++jj) {
IYREB[jj]= IYREB[kk= jj+1];
RXREB[jj]= RXREB[kk];
RPRIR[jj]= RPRIR[kk];
}
goto M2;
WYBROSILI:
ibgind+= ikledg;
iytek= iysled;
goto FORM_EDGES;
KOHGFA:;
} /* V_FP0 */
/*---------------------------------------------- main V_FP0 */
float Px[MAXARR] = {
0.0,200.0,200.0,250.0,270.0,270.0,210.0,210.0,230.0,230.0
};
float Py[MAXARR] = {
0.0,200.0,250.0,250.0,230.0,200.0,210.0,230.0,230.0,210.0
};
void main (void)
{
int ii, kol, grn, new, entry;
int gdriver = DETECT, gmode;
kol= 5; /* Кол-во вершин */
grn= 11; /* Код пикселов границы */
new= 14; /* Код заливки */
entry= 1;
initgraph(&gdriver, &gmode, "c:\tc\bgi");
if ((ii= graphresult()) != grOk) {
printf ("Err=%d\n", ii); goto all;
}
m0:goto m2;
m1:++entry;
printf("Vertexs, boundary_pixel, pixel= (%d %d %d) ? ",
kol, grn, new);
scanf ("%d%d%d", &kol, &grn, &new);
if (kol < 0) goto all;
for (ii=1; ii<=kol; ++ii) {
printf ("Px[%d], Py[%d] = ? ", ii, ii);
scanf ("%d%d", &Px[ii], &Py[ii]);
}
m2:
setbkcolor(0); /* Очистка экрана */
cleardevice();
/* Заливка */
V_FP0 (new, kol, Px, Py);
/* Построение границы */
setcolor (grn);
for (ii= 1; ii<kol; ++ii)
line (Px[ii], Py[ii], Px[ii+1], Py[ii+1]);
line (Px[kol], Py[kol], Px[1], Py[1]);
/* При первом входе строится квадратик дырки */
if (!entry) {
for (ii=kol+1; ii<kol+4; ++ii)
line (Px[ii], Py[ii], Px[ii+1], Py[ii+1]);
line (Px[kol+4], Py[kol+4], Px[kol+1], Py[kol+1]);
}
goto m1;
all:
closegraph();
}
/*===================================================== V_FP1
* Более эффективная по сравнению с V_FP0 подпрограмма
* однотонной заливки многоугольника методом построчного
* сканирования.
*
* Дублирувание занесения пикселов практически отсутствует
*
*/
#include <stdio.h>
#include <graphics.h>
#define MAXARR 300 /* Макс кол-во вершин многоугольника */
#define MAXLST 300 /* Макс размер списка активных ребер */
/*---------------------------------------------------- FILSTR
* Заливает строку iy от ixn до ixk
*
* void FILSTR (int kod, int iy, int ixn, int ixk)
*/
void FILSTR (kod, iy, ixn, ixk)
int kod, iy, ixn, ixk;
{
while (ixn <= ixk) putpixel (ixn++, iy, kod);
} /* FILSTR */
/*--------------- Глобалы процедуры закраски ---------------*/
static int KOD, NWER; /* Код заливки и кол-во вершин */
static float *pt_X; /* Массивы входных координат вершин */
static float *pt_Y;
static int IBGIND; /* Номер след вершины в списке */
static int IEDG[MAXARR]; /* Y-коорд вершин по возрастан */
static int INOM[MAXARR]; /* и их номера в исх масс Py */
/* Список активных ребер */
static int IDLSPI; /* Длина списка активных ребер */
static int IYREB[MAXLST]; /* Макс Y-коорд активных ребер */
static float RXREB[MAXLST]; /* Тек X-коорд активных ребер */
static float RPRIR[MAXLST]; /* Х-приращение на 1 шаг по Y */
static float RYSL[MAXLST]; /* Dy между тек и соседн верш */
/* Dy <= 0.0 - обычная вершина */
/* > 0.0 - локал экстремум */
/*---------------------------------------------------- FORSPI
* int FORSPI (int IYBEG)
*
* 1) Формирует элементы списка для ребер,
* начинающихся в IYBEG;
* 2) Вычиcляeт IBGIND - индeкc нaчaлa следующей
* вepшины в cпиcкe вepшин;
* 3) Возвращает IYSLED - Y кoopдинaтy ближaйшeй
* вepшины, дo кoтopoй мoжнo зaливaть бeз
* пepecтpoйки cпиcкa.
*
* Глoбaльныe вeличины :
*
* KOD - код заливки
* NWER - кoл-вo вepшин в иcxoднoм мнoгoyгoльникe,
* *pt_X - X-кoopдинaты иcxoднoгo мнoгoyгoльника,
* *pt_Y - Y-кoopдинaты иcxoднoгo мнoгoyгoльника,
* IEDG - yпopядoчeнный пo вoзpacтaнию мaccив
* Y кoopдинaт вepшин иcxoднoгo мнoгoyгoльн
* INOM - INOM[i] зaдaeт нoмep вepшины в иcxoднoм
* мнoгoyгoльникe для IEDG[i],
* IBGIND - индeкc мaccивoв IEDG, INOM
* oпpeдeляeт гдe мoжeт нaчaтьcя ребpo,
* IDLSPI - длинa пocтpoeннoгo cпиcкa aктивныx ребep,
* cocтoящeгo из :
* IYREB - мaкc кoopдинaты ребep,
* RXREB - внaчaлe мин, зaтeм тeкyщaя X-кoopдинaтa,
* RPRIR - пpиpaщeниe к X-кoopдинaтe нa 1 шaг пo Y,
* RYSL - пpизнaк тoгo чтo зa вepшинa :
* <= 0 - oбычнaя,
* > 0 - лoкaльный экcтpeмyм
* пepeceчeниe cтpoки зaкpacки
* c экcтpeмyмoм cчитaeтcя зa 2 тoчки,
* c oбычнoй - зa 1;
*/
static int FORSPI (IYBEG)
int IYBEG;
{
int i,ikledg,intek,intabs,isd;
int iyt,ixt,nrebra,inc,inpred,inposl;
float xt, xc, yt, yc, dy;
/* ikledg = кoл-вo вepшин c дaнным IYBEG */
ikledg= 0;
for (i=IBGIND; i<=NWER; ++i)
if (IEDG[i] != IYBEG) break; else ++ikledg;
/* Цикл пocтpoeния cпиcкa aктивныx ребep
и зaкpaшивaниe гopизонтальных ребep
*/
for (i=1; i<=ikledg; ++i) {
/* Bычисл номера текущей вершины */
intek= INOM[IBGIND+i-1];
intabs= abs (intek);
xt= pt_X[intabs];
yt= pt_Y[intabs];
/* Bычисл номеров предыд и послед вершин */
if ((inpred= intabs - 1) < 1) inpred= NWER;
if ((inposl= intabs + 1) > NWER) inposl= 1;
/*
* По заданным :
* NWER - кол-во вершин,
* intek - номер текущей вершины,
* isd = 0/1 - правилу выбора соседней вершины -
* предыдущая/последующая
* вычиcляeт dy,
* Еcли dy < 0 тo вepшинa yжe oбpaбoтaнa,
* Еcли dy == 0 тo вepшины нa oдном Y
* Пpи этoм cтpoитcя гopизoнтaльный oтpeзoк.
* Фaкт зaкpacки гopизoнтaльнoгo ребpa
* oтмeчaeтcя oтpицaтeльным знaчeниeм
* cooтвeтcтвyющeгo знaчeния INOM.
* Еcли dy > 0 тo фopмиpyeтcя нoвый элeмент cпиcкa
* aктивныx ребep
*/
for (isd=0; isd<=1; ++isd) {
if (!isd) nrebra= inc= inpred; else {
inc= inposl; nrebra= intabs;
}
yc= pt_Y[inc];
dy= yc - yt;
if (dy < 0.0) continue;
xc= pt_X[inc];
if (dy != 0.0) goto DYNE0;
if ((inc= INOM[nrebra]) < 0) continue;
INOM[nrebra]= -inc;
iyt= yt;
inc= xc;
ixt= xt;
FILSTR (KOD, iyt, inc, ixt);
continue;
DYNE0: ++IDLSPI;
IYREB[IDLSPI]= yc;
RXREB[IDLSPI]= xt;
RPRIR[IDLSPI]= (xc - xt) / dy;
inc= (!isd) ? inposl : inpred;
RYSL[IDLSPI]= pt_Y[inc] - yt;
} /* цикла по isd */
} /* построения списка активных ребер */
/* Bычисление Y ближайшей вершины */
if ((i= (IBGIND += ikledg)) > NWER) i= NWER;
return (IEDG[i]);
} /* Процедуры FORSPI */
/*----------------------------------------------------- V_FP1
* Однотонно заливает многоугольник,
* заданный координатами вершин
*
* void V_FP1 (int pixel, int kol, float *Px, float *Py)
*
*/
void V_FP1 (pixel, kol, Px, Py)
int pixel, kol; float *Px, *Py;
{
int i,j,k,l;
int iytek; /* Y текущей строки сканирования */
int iymin; /* Y-мин при сортировке массива Y-коорд */
int iybeg; /* Мин Y-координата заливки */
int iymak; /* Max Y-координата заливки */
int iysled; /* Y кoopд ближaйшeй вepшины, дo кoтopoй */
/* можно зaливaть бeз пepecтpoйки cпиcкa */
int newysl;
int ixmin; /* X-мин при сортировке для тек строки */
int ixtek; /* X-тек при сортировке для тек строки */
int irabx[MAXLST]; /* X-коорд пересечений в строке сканир */
KOD= pixel; /* Параметры в глобалы */
NWER= kol;
pt_X= Px;
pt_Y= Py;
/* Построение массивов Y и их номеров */
for (i= 1; i<=NWER; ++i) {IEDG[i]= Py[i]; INOM[i]= i; }
/* Cовместная сортировка массивов IEDG, IHOM */
for (i= 1; i<=NWER; ++i) {
iymin= IEDG[i];
k= 0;
for (j=i+1; j<=NWER; ++j)
if ((l= IEDG[j]) < iymin) {iymin= l; k= j; }
if (k) {
IEDG[k]= IEDG[i]; IEDG[i]= iymin;
iymin= INOM[k];
INOM[k]= INOM[i]; INOM[i]= iymin;
}
}
/* Hачальные присвоения */
IDLSPI= 0;
IBGIND= 1;
iybeg= IEDG[1];
iymak= IEDG[NWER];
/* Формирование начального списка акт ребер */
iysled= FORSPI (iybeg);
if (!IDLSPI) goto KOHGFA;
/* Горизонтальная раскраска по списку */
ZALIWKA:
for (iytek=iybeg; iytek<=iysled; ++iytek) {
if (iytek == iysled) { /* Y-координата перестройки */
newysl= FORSPI (iytek);
if (!IDLSPI) goto KOHGFA;
}
/* Bыборка и сортировка X-ов из списка ребер */
l= 0;
for (i=1; i<=IDLSPI; ++i)
if (RYSL[i] > 0.0) irabx[++l]= RXREB[i];
else RYSL[i]= 1.0;
for (i=1; i<=l; ++i) {
ixmin= irabx[i];
k= 0;
for (j=i+1; j<=l; ++j) {
ixtek= irabx[j];
if (ixtek < ixmin) {k= j; ixmin= ixtek; }
}
if (k) {irabx[k]= irabx[i]; irabx[i]= ixmin; }
} /* цикла сортировки */
/* Cобственно заливка */
for (j=1; j<=l-1; j+= 2)
FILSTR (KOD,iytek,irabx[j],irabx[j+1]);
for (j=1; j<=IDLSPI; ++j) /* Приращения X-ов */
RXREB[j]= RXREB[j] + RPRIR[j];
} /* цикла горизонтальной раскраски */
if (iysled == iymak) goto KOHGFA;
/* Bыбрасывание из списка всех ребер с YMAK ребра == YSLED */
i= 0;
M1:++i;
M2:if (i > IDLSPI) goto WYBROSILI;
if (IYREB[i] != iysled) goto M1;
--IDLSPI;
for (j=i; j<=IDLSPI; ++j) {
IYREB[j]= IYREB[k= j+1];
RXREB[j]= RXREB[k];
RPRIR[j]= RPRIR[k];
}
goto M2;
WYBROSILI:
iybeg= iysled + 1;
iysled= newysl;
goto ZALIWKA;
KOHGFA:;
} /* V_FP1 */
/*---------------------------------------------- main V_FP1 */
float Px[MAXARR] = {
0.0,200.0,200.0,250.0,270.0,270.0,210.0,210.0,230.0,230.0
};
float Py[MAXARR] = {
0.0,200.0,250.0,250.0,230.0,200.0,210.0,230.0,230.0,210.0
};
void main (void)
{
int ii, kol, grn, new, entry;
int gdriver = DETECT, gmode;
kol= 5; /* Кол-во вершин */
grn= 11; /* Код пикселов границы */
new= 14; /* Код заливки */
entry= 1;
initgraph(&gdriver, &gmode, "c:\tc\bgi");
if ((ii= graphresult()) != grOk) {
printf ("Err=%d\n", ii); goto all;
}
m0:goto m2;
m1:++entry;
printf("Vertexs, boundary_pixel, pixel= (%d %d %d) ? ",
kol, grn, new);
scanf ("%d%d%d", &kol, &grn, &new);
if (kol < 0) goto all;
for (ii=1; ii<=kol; ++ii) {
printf ("Px[%d], Py[%d] = ? ", ii, ii);
scanf ("%d%d", &Px[ii], &Py[ii]);
}
m2:
setbkcolor(0); /* Очистка экрана */
cleardevice();
/* Заливка */
V_FP1 (new, kol, Px, Py);
/* Построение границы */
setcolor (grn);
for (ii= 1; ii<kol; ++ii)
line (Px[ii], Py[ii], Px[ii+1], Py[ii+1]);
line (Px[kol], Py[kol], Px[1], Py[1]);
/* При первом входе строится квадратик дырки */
if (!entry) {
for (ii=kol+1; ii<kol+4; ++ii)
line (Px[ii], Py[ii], Px[ii+1], Py[ii+1]);
line (Px[kol+4], Py[kol+4], Px[kol+1], Py[kol+1]);
}
goto m1;
all:
closegraph();
}
В данном приложении приведены три процедуры заливки гранично-определенной области с затравкой.
Первая процедура - V_FAB4R реализует рекурсивный алгоритм заполнения для 4-х связной области соответствующий алгоритму, помещенному в [4].
Вторая процедура - V_FAB4 реализует итеративный алгоритм заполнения для 4-х связной области близкий к алгоритму, помещенному в [3].
Характерная особенность таких алгоритмов - очень большие затраты памяти под рабочий стек и многократное дублирование занесения пикселов. Характерные значения для размера стека (см. ниже определение константы MAX_STK) около десяти тысяч байт при размере порядка 70×70 пикселов и очень сильно зависят от размеров заливаемой области, ее конфигурации и выбора начальной точки. Так, например, для заливки квадрата со стороной, равной 65 дискретам, и старте заливки из точки (20,20) относительно угла квадрата требуется 7938 байт для стека.
Третья процедура - V_FAST реализует алгоритм построчного заполнения с затравкой гранично-определенной области, близкий к соответствующему алгоритму из [3]. Отличительная черта таких алгоритмов - большие объемы программного кода, небольшие затраты памяти под рабочий стек и практически отсутствующее дублирование занесения пикселов. Характерные значения для размера стека (см. ниже определение константы MAX_STK) около сотни байт.
/*---------------------------------------------------- V_FAB4R
* Подпрограммы для заливки с затравкой гранично-определенной
* области 4-х связным алгоритмом:
*
* V_FAB4R - заливка гранично-определенной
* области 4-х связным алгоритмом
*/
#include <graphics.h>
#include <stdio.h>
#define MAX_GOR 2048 /* Разрешение дисплея по X */
#define MAX_VER 2048 /* Разрешение дисплея по Y */
static int gor_max= MAX_GOR;
static int ver_max= MAX_VER;
/*---------------------------------------------------- V_FAB4R
* Заливка гранично-определенной области
* 4-х связным алгоритмом
*/
void V_FAB4R (grn_pix, new_pix, x_isx, y_isx)
int grn_pix, new_pix, x_isx, y_isx;
{
if (getpixel (x_isx, y_isx) != grn_pix &&
getpixel (x_isx, y_isx) != new_pix)
{
putpixel (x_isx, y_isx, new_pix);
V_FAB4R (grn_pix, new_pix, x_isx+1, y_isx);
V_FAB4R (grn_pix, new_pix, x_isx, y_isx+1);
V_FAB4R (grn_pix, new_pix, x_isx-1, y_isx);
V_FAB4R (grn_pix, new_pix, x_isx, y_isx-1);
}
} /* V_FAB4 */
/*-------------------------------------------------- FAB4_MAIN
*/
void main (void)
{
int ii, kol, grn, new, entry;
int x_isx, y_isx;
int gdriver = DETECT, gmode;
int Px[256] = {200,200,250,270,270,210,210,230,230};
int Py[256] = {200,250,250,230,200,210,230,230,210};
kol= 5; /* Кол-во вершин */
grn= 11; /* Код пикселов границы */
new= 14; /* Код заливки */
x_isx= 240; /* Координаты затравки */
y_isx= 240;
entry= 0;
initgraph(&gdriver, &gmode, "c:\tc\bgi");
if ((ii= graphresult()) != grOk) {
printf ("Err=%d\n", ii); goto all;
}
m0:goto m2;
m1:++entry;
printf("Vertexs, boundary_pixel, new_pixel= (%d %d %d) ? ",
kol, grn, new);
scanf ("%d%d%d", &kol, &grn, &new);
if (kol < 0) goto all;
for (ii=0; ii<kol; ++ii) {
printf ("Px[%d], Py[%d] = ? ", ii, ii);
scanf ("%d%d", &Px[ii], &Py[ii]);
}
printf ("X,Y isx= (%d %d) ? ", x_isx, y_isx);
scanf ("%d%d", &x_isx, &y_isx);
m2:
setbkcolor(0);
cleardevice();
/* Построение границы */
setcolor (grn);
for (ii= 0; ii<kol-1; ++ii)
line (Px[ii], Py[ii], Px[ii+1], Py[ii+1]);
line (Px[kol-1], Py[kol-1], Px[0], Py[0]);
/* При первом входе строится квадратик дырки */
if (!entry) {
for (ii= kol; ii<kol+3; ++ii)
line (Px[ii], Py[ii], Px[ii+1], Py[ii+1]);
line (Px[kol+3], Py[kol+3], Px[kol], Py[kol]);
}
/* Заливка */
V_FAB4R (grn, new, x_isx, y_isx);
goto m1;
all:
closegraph();
}
/*----------------------------------------------------- V_FAB4
* Подпрограммы для заливки с затравкой гранично-определенной
* области 4-х связным алгоритмом:
*
* Pop_Stk - Локальная подпрограмма. Извлекает координаты
* пиксела из стека в глобальные скаляры xtek, ytek
*
* Push_Stk - Локальная подпрограмма. Заносит координаты
* пиксела в стек
*
* V_FAB4 - собственно заливка гранично-определенной
* области 4-х связным алгоритмом
*
* V_FA_SET - устанавливает количественные ограничения
* для заливки
*/
#include <alloc.h>
#include <graphics.h>
#include <stdio.h>
#define MAX_GOR 2048 /* Разрешение дисплея по X */
#define MAX_VER 2048 /* Разрешение дисплея по Y */
#define MAX_STK 8192 /* Размер стека координат заливки */
static int gor_max= MAX_GOR;
static int ver_max= MAX_VER;
static int stk_max= MAX_STK;
static int *pi_stk, *pn_stk; /* Указ стека заливки */
static int xtek, ytek; /* Координаты из стека */
static int stklen; /* Достигнутая глубина стека*/
/* только для отладочных */
/* измерений программы */
/*---------------------------------------------------- Pop_Stk
* Извлекает координаты пиксела из стека в xtek, ytek
* Возвращает 0/1 - нет/есть ошибки
*/
static int Pop_Stk ()
{ register int otw;
otw= 0;
if (pi_stk <= pn_stk) ++otw; else {
ytek= *--pi_stk; xtek= *--pi_stk;
}
return (otw);
} /* Pop_Stk */
/*--------------------------------------------------- Push_Stk
* Заносит координаты пиксела в стек
* Возвращает -1/0 - нет места под стек/норма
*/
static int Push_Stk (x, y)
register int x, y;
{
register int glu;
if ((glu= pi_stk - pn_stk) >= stk_max) x= -1; else {
*pi_stk++= x; *pi_stk++= y; x= 0;
if (glu > stklen) stklen= glu;
}
return (x);
} /* Push_Stk */
/*----------------------------------------------------- V_FAB4
* Заливка гранично-определенной области
* 4-х связным алгоритмом
* Возвращает:
* -1 - нет места под стек
* 0 - норма
*/
int V_FAB4 (grn_pix, new_pix, x_isx, y_isx)
int grn_pix, new_pix, x_isx, y_isx;
{
register int pix, x, y, otw;
otw= 0;
/* Инициализация стека */
if ((pn_stk= (int *)malloc (stk_max)) == NULL) {
--otw; goto all;
}
pi_stk= pn_stk;
Push_Stk (x_isx, y_isx); /* Затравку в стек */
while (pn_stk < pi_stk) { /* Пока не исчерпан стек */
/* Выбираем пиксел из стека и красим его */
Pop_Stk ();
if (getpixel (x= xtek, y= ytek) != new_pix)
putpixel (x, y, new_pix);
/* Проверяем соседние пикселы на необходимость закраски */
if ((pix= getpixel (++x, y)) != new_pix &&
pix != grn_pix) otw= Push_Stk (x, y);
if ((pix= getpixel (--x, ++y)) != new_pix &&
pix != grn_pix) otw= Push_Stk (x, y);
if ((pix= getpixel (--x, --y)) != new_pix &&
pix != grn_pix) otw= Push_Stk (x, y);
if ((pix= getpixel (++x, --y)) != new_pix &&
pix != grn_pix) otw= Push_Stk (x, y);
if (otw) break;
}
all:
free (pn_stk);
return (otw);
} /* V_FAB4 */
/*--------------------------------------------------- V_FA_SET
* Устанавливает количественные ограничения для заливки
*/
void V_FA_SET (x_resolution, y_resolution, stack_length)
int x_resolution, y_resolution, stack_length;
{
if (x_resolution > 0 && x_resolution <= MAX_GOR)
gor_max= x_resolution;
if (y_resolution > 0 && y_resolution <= MAX_VER)
ver_max= y_resolution;
/* Кол байт координат, заносимых в стек м.б. только четным */
if (stack_length > 0) stk_max= stack_length & 0177776;
} /* V_FA_SET */
/*-------------------------------------------------- FAB4_MAIN
*/
void main (void)
{
int ii, kol, grn, new, entry;
int x_isx, y_isx;
int gdriver = DETECT, gmode;
int Px[256] = {200,200,250,270,270,210,210,230,230};
int Py[256] = {200,250,250,230,200,210,230,230,210};
kol= 5; /* Кол-во вершин */
grn= 11; /* Код пикселов границы */
new= 14; /* Код заливки */
x_isx= 240; /* Координаты затравки */
y_isx= 240;
entry= 0;
initgraph(&gdriver, &gmode, "c:\tc\bgi");
if ((ii= graphresult()) != grOk) {
printf ("Err=%d\n", ii); goto all;
}
m0:goto m2;
m1:++entry;
printf("Vertexs, boundary_pixel, new_pixel= (%d %d %d) ? ",
kol, grn, new);
scanf ("%d%d%d", &kol, &grn, &new);
if (kol < 0) goto all;
for (ii=0; ii<kol; ++ii) {
printf ("Px[%d], Py[%d] = ? ", ii, ii);
scanf ("%d%d", &Px[ii], &Py[ii]);
}
printf ("X,Y isx= (%d %d) ? ", x_isx, y_isx);
scanf ("%d%d", &x_isx, &y_isx);
m2:
setbkcolor(0);
cleardevice();
/* Построение границы */
setcolor (grn);
for (ii= 0; ii<kol-1; ++ii)
line (Px[ii], Py[ii], Px[ii+1], Py[ii+1]);
line (Px[kol-1], Py[kol-1], Px[0], Py[0]);
/* При первом входе строится квадратик дырки */
if (!entry) {
for (ii= kol; ii<kol+3; ++ii)
line (Px[ii], Py[ii], Px[ii+1], Py[ii+1]);
line (Px[kol+3], Py[kol+3], Px[kol], Py[kol]);
}
/* Установка количественных ограничений для проц заливки */
V_FA_SET (getmaxx()+1, getmaxy()+1, MAX_STK);
stklen= 0; /* Занятое кол-во байт в стеке */
/* Заливка */
ii= V_FAB4 (grn, new, x_isx, y_isx);
printf ("Answer= %d MaxStack=%d\n", ii, stklen);
goto m1;
all:
closegraph();
}
/*----------------------------------------------------- V_FAST
* Подпрограммы заливки области с затравкой
* построчным алгоритмом:
*
* Pop_Stk - Локальная подпрограмма. Извлекает координаты
* пиксела из стека в глобальные скаляры xtek,ytek
*
* Push_Stk - Локальная подпрограмма. Заносит координаты
* пиксела в стек
*
* Get_Video - Локальная подпрограмма. Читает строку из
* видеопамяти в глобальный буфер строки.
*
* Put_Video - Локальная подпрограмма. Копирует байты из
* глобального буфера строки в видеопамять.
*
* Search - Локальная подпрограмма. Ищет затравочные
* пикселы в строке видеопамяти, находящейся
* в глобальном массиве.
*
* V_FAST - Собственно подпрограмма построчной заливки
* гранично-определенной области
*
* V_FA_SET - Устанавливает количественные ограничения
* для заливки
*/
#include <alloc.h>
#include <graphics.h>
#include <stdio.h>
#define MAX_GOR 2048 /* Разрешение дисплея по X */
#define MAX_VER 2048 /* Разрешение дисплея по Y */
#define MAX_STK 8192 /* Размер стека координат заливки */
static int gor_max= MAX_GOR;
static int ver_max= MAX_VER;
static int stk_max= MAX_STK;
static int *pi_stk, *pn_stk; /* Указ стека заливки */
static int xtek, ytek; /* Координаты из стека */
static char *pc_video; /* Указ на буфер строки */
static int stklen; /* Достигнутая глубина стека*/
/* только для отладочных */
/* измерений программы */
/*---------------------------------------------------- Pop_Stk
* Извлекает координаты пиксела из стека в xtek, ytek
* Возвращает 0/1 - нет/есть ошибки
*/
static int Pop_Stk ()
{ register int otw;
otw= 0;
if (pi_stk <= pn_stk) ++otw; else {
ytek= *--pi_stk; xtek= *--pi_stk;
}
return (otw);
} /* Pop_Stk */
/*--------------------------------------------------- Push_Stk
* Заносит координаты пиксела в стек
* Возвращает -1/0 - нет места под стек/норма
*/
static int Push_Stk (x, y)
register int x, y;
{
register int glu;
if ((glu= pi_stk - pn_stk) >= stk_max) x= -1; else {
*pi_stk++= x; *pi_stk++= y; x= 0;
if (glu > stklen) stklen= glu;
}
return (x);
} /* Push_Stk */
/*-------------------------------------------------- Get_Video
* В байтовый буфер строки, заданный глобальным
* указателем pc_video,
* читает из видеопамяти пикселы y-строки от xbg до xen
* Возвращает 0/1 - нет/есть ошибки
*/
static int Get_Video (y, pcxbg, pcxen)
int y; register char *pcxbg, *pcxen;
{ register int x;
if (y>=0 && y<ver_max && pcxbg<=pcxen) {
x= pcxbg - pc_video;
do *pcxbg++= getpixel (x++, y); while (pcxbg <= pcxen);
y= 0;
} else y= 1;
return (y);
} /* Get_Video */
/*-------------------------------------------------- Put_Video
* Пикселы из буфера строки, начиная от указателя pxbg,
* до указателя pxen пишет в y-строку видеопамяти
* Возвращает 0/1 - нет/есть ошибки
*/
static int Put_Video (y, pxbg, pxen)
int y; register char *pxbg, *pxen;
{ register int x;
if (y>=0 && y<ver_max && pxbg<=pxen) {
x= pxbg - pc_video;
do putpixel (x++, y, *pxbg++); while (pxbg <= pxen);
y= 0;
} else y= 1;
return (y);
} /* Put_Video */
/*----------------------------------------------------- Search
* Ищет затравочные пикселы в yt-строке видеопамяти,
* находящейся по указателю pc_video, начиная от
* указателя pcl до указателя pcr
* grn - код граничного пиксела
* new - код, которым перекрашивается область
* Возвращает: 0/1 - не найден/найден затравочный
*/
static int Search (yt, pcl, pcr, grn, new)
int yt; char *pcl, *pcr; int grn, new;
{ register int pix;
register char *pc;
int x, otw;
otw= 0;
while (pcl <= pcr) {
pc= pcl; /* Указ тек пиксела */
/* Поиск крайнего правого не закрашенного пиксела в строке */
while ((pix= *pc & 255) != grn && pix != new && pc<pcr)
++pc;
if (pc != pcl) { /* Найден закрашиваемый */
++otw;
x= pc - pc_video; /* Его координата в строке */
if (pc != pcr || pix == grn || pix == new) --x;
Push_Stk (x, yt);
}
/* Продолжение анализа строки пока не достигнут прав пиксел */
pcl= pc;
while (((pix= *pc & 255) == grn || pix==new) && pc<pcr)
++pc;
if (pc == pcl) ++pc;
pcl= pc;
}
return (otw);
} /* Search */
/*----------------------------------------------------- V_FAST
* Построчная заливка с затравкой гранично-определенной
* области
*
* int V_FAST (int grn_pix, int new_pix, int x_isx, int y_isx)
*
* Вход:
* grn_pix - код граничного пиксела
* new_pix - код заполняющего пиксела
* x_isx - координаты затравки
* y_isx
*
* Возвращает:
* -2 - нет места под растровую строку
* -1 - нет места под стек
* 0 - норма
* 1 - при чтении пикселов из видеопамяти в буферную
* строки выход за пределы буферной строки
* 2 - исчерпан стек при запросе координат пикселов
*
*/
int V_FAST (grn_pix, new_pix, x_isx, y_isx)
int grn_pix, new_pix, x_isx, y_isx;
{
register char *pcl; /* Указ левого пиксела в строке */
register char *pcr; /* Указ правого пиксела в строке */
int otw;
otw= 0;
/* Инициализация стека */
if ((pn_stk= (int *)malloc (stk_max)) == NULL) {
--otw; goto all;
}
pi_stk= pn_stk;
/* Заказ массива под растровую строку */
if ((pc_video= malloc (gor_max)) == NULL) {
otw= -2; goto fre_stk;
}
Push_Stk (x_isx, y_isx); /* Затравку в стек */
/* Цикл заливки строк до исчерпания стека */
while (pi_stk > pn_stk) {
/* Запрос координат затравки из стека */
if (Pop_Stk ()) {otw=2; break; }
pcl= pcr= pc_video + xtek; /* Указ затравки */
/* Запрос полной строки из видеопамяти */
if (Get_Video (ytek, pc_video, pc_video+gor_max-1))
{otw= 1; break; }
/* Закраска затравки и вправо от нее */
do *pcr++= new_pix; while ((*pcr & 255) != grn_pix);
--pcr; /* Указ крайнего правого */
/* Закраска влево */
while ((*--pcl & 255) != grn_pix) *pcl= new_pix;
++pcl; /* Указ крайнего левого */
/* Занесение подправленной строки в видеопамять */
Put_Video (ytek, pcl, pcr);
/* Поиск затравок в строках ytek+1 и ytek-1,
* начиная с левого подинтервала, заданного pcl, до
* правого подинтервала, заданного pcr
*/
if (!Get_Video (++ytek, pcl, pcr))
Search (ytek, pcl, pcr, grn_pix, new_pix);
if (!Get_Video (ytek-= 2, pcl, pcr))
Search (ytek, pcl, pcr, grn_pix, new_pix);
}
free (pc_video);
fre_stk:
free (pn_stk);
all:
return (otw);
} /* V_FAST */
/*--------------------------------------------------- V_FA_SET
* Устанавливает количественные ограничения для заливки
*/
void V_FA_SET (x_resolution, y_resolution, stack_length)
int x_resolution, y_resolution, stack_length;
{
if (x_resolution > 0 && x_resolution <= MAX_GOR)
gor_max= x_resolution;
if (y_resolution > 0 && y_resolution <= MAX_VER)
ver_max= y_resolution;
/* Кол байт координат, заносимых в стек м.б. только четным */
if (stack_length > 0) stk_max= stack_length & 0177776;
} /* V_FA_SET */
/*-------------------------------------------------- FAST_MAIN
*/
void main (void)
{
int ii, kol, grn, new, entry;
int x_isx, y_isx;
int gdriver = DETECT, gmode;
int Px[256] = {200,200,250,270,270,210,210,230,230};
int Py[256] = {200,250,250,230,200,210,230,230,210};
kol= 5; /* Кол-во вершин */
grn= 11; /* Код пикселов границы */
new= 14; /* Код заливки */
x_isx= 240; /* Координаты затравки */
y_isx= 240;
entry= 0;
initgraph(&gdriver, &gmode, "c:\tc\bgi");
if ((ii= graphresult()) != grOk) {
printf ("Err=%d\n", ii); goto all;
}
m0:goto m2;
m1:++entry;
printf("Vertexs, boundary_pixel, new_pixel= (%d %d %d) ? ",
kol, grn, new);
scanf ("%d%d%d", &kol, &grn, &new);
if (kol < 0) goto all;
for (ii=0; ii<kol; ++ii) {
printf ("Px[%d], Py[%d] = ? ", ii, ii);
scanf ("%d%d", &Px[ii], &Py[ii]);
}
printf ("X,Y isx= (%d %d) ? ", x_isx, y_isx);
scanf ("%d%d", &x_isx, &y_isx);
m2:
setbkcolor(0);
cleardevice();
/* Построение границы */
setcolor (grn);
for (ii= 0; ii<kol-1; ++ii)
line (Px[ii], Py[ii], Px[ii+1], Py[ii+1]);
line (Px[kol-1], Py[kol-1], Px[0], Py[0]);
/* При первом входе строится квадратик дырки */
if (!entry) {
for (ii= kol; ii<kol+3; ++ii)
line (Px[ii], Py[ii], Px[ii+1], Py[ii+1]);
line (Px[kol+3], Py[kol+3], Px[kol], Py[kol]);
}
/* Установка количественных ограничений для проц заливки */
V_FA_SET (getmaxx()+1, getmaxy()+1, MAX_STK);
stklen= 0; /* Занятое кол-во байт в стеке */
/* Заливка */
ii= V_FAST (grn, new, x_isx, y_isx);
printf ("Answer= %d MaxStack=%d\n", ii, stklen);
goto m1;
all:
closegraph();
}
В данном приложении приведены процедуры, обеспечивающие выполнение отсечения по прямоугольному и многоугольному выпуклому окну и тестовая программа проверки работы процедур отсечения.
/*=================================================== V_CLIP.C
*
* Подрограммы, связанные с отсечением:
*
* V_SetPclip - установить размеры многоугольного окна
* отсечения
* V_SetRclip - установить размеры прямоугольного окна
* отсечения
* V_GetRclip - опросить размеры прямоугольного окна
* отсечения
* V_CSclip - отсечение по алгоритму Коэна-Сазерленда
* прямоугольное окно, кодирование
* концов отсекаемого отрезка
* V_FCclip - отсечение по алгоритму быстрого отсечения
* Алгоритм Собкова-Поспишила-Янга -
* прямоугольное окно, кодирование
* отсекаемого отрезка
* V_LBclip - отсечение по алгоритму Лианга-Барски
* прямоугольное окно, параметрическое
* представление линий
* V_CBclip - отсечение по алгоритму Кируса-Бека
* окно - выпуклый многоугольник,
* параметрическое представление линий
*/
/* Глобальные скаляры для алгоритмов отсечения по
* прямоугольному окну - Коэна-Сазерленда, Fc-алгоритм,
* Лианга-Барски
*/
static float Wxlef= 0.0, /* Координаты левого нижнего и */
Wybot= 0.0, /* правого верхнего углов окна */
Wxrig= 7.0, /* отсечения */
Wytop= 5.0;
/* Глобальные скаляры для алгоритма Кируса-Бека
* отсечения по многоугольному окну
*/
/* Координаты прямоугольного окна */
static float Wxrect[4]= {0.0, 0.0, 7.0, 7.0 };
static float Wyrect[4]= {0.0, 5.0, 5.0, 0.0 };
/* Перепендикуляры к сторонам прямоугольного окна */
static float WxNrec[4]= {1.0, 0.0, -1.0, 0.0 };
static float WyNrec[4]= {0.0, -1.0, 0.0, 1.0 };
/* Данные для многоугольного окна */
static int Windn=4; /* Кол-во вершин у окна */
static float *Windx= Wxrect, /* Координаты вершин окна */
*Windy= Wyrect;
static float *Wnormx= WxNrec, /* Координаты нормалей */
*Wnormy= WyNrec;
/*------------------------------------------------- V_SetPclip
* Устанавливает многоугольное окно отсечения
* kv - количество вершин в окне
* wx - X-координаты вершин
* wy - Y-координаты вершин
* nx - X-координаты нормалей к ребрам
* ny - Y-координаты нормалей к ребрам
*
* Проверяет окно на выпуклость и невырожденность
*
* Если окно правильное, то
* 1. Обновляет глобалы описания многоугольного окна:
* Windn= kv;
* Windx= wx; Windy= wy; --Координаты вершин окна
* Wnormx= nx; Wnormy= ny; --Координаты перпендикуляров
*
* 2. Вычисляет координаты перепендикуляров к сторонам окна
*
* Возвращает:
* 0 - норма
* 1 - вершин менее трех
* 2 - многоугольник вырожден в отрезок
* 3 - многоугольник невыпуклый
*/
int V_SetPclip (kv, wx, wy, nx, ny)
int kv; float *wx, *wy, *nx, *ny;
{ int ii, jj, sminus, splus, szero, otw;
float r,
vox, voy, /* Координаты (i-1)-й вершины */
vix, viy, /* Координаты i-й вершины */
vnx, vny; /* Координаты (i+1)-й вершины */
/* Проверка на выпуклость
* для этого вычисляются векторные произведения
* смежных сторон и определяется знак
* если все знаки == 0 то многоугольник вырожден
* если все знаки >= 0 то многоугольник выпуклый
* если все знаки <= 0 то многоугольник невыпуклый
*/
otw= 0;
if (--kv < 2) {++otw; goto all; }
sminus= 0;
splus= 0;
szero= 0;
vox= wx[kv]; voy= wy[kv];
vix= *wx; viy= *wy;
ii= 0;
do {
if (++ii > kv) ii= 0; /* Следующая вершина */
vnx= wx[ii]; vny= wy[ii]; /* Координаты (i+1)-й */
r= (vix-vox)*(vny-viy) - /* Вект произв ребер */
(viy-voy)*(vnx-vix); /* смежных с i-й верш */
if (r < 0) ++sminus; else
if (r > 0) ++splus; else ++szero;
vox= vix; voy= viy; /* Обновлен координат */
vix= vnx; viy= vny;
} while (ii);
if (!splus && !sminus) /* Все векторные равны нулю */
{otw= 2; goto all; } /* Многоугольник вырожден */
if (splus && sminus) /* Знакопеременн. векторные */
{otw= 3; goto all; } /* Многоугольник невыпуклый */
/* Установление глобалов для правильного окна */
Windn= kv+1; /* Количество вершин у окна */
Windx= wx; Windy= wy; /* Координаты вершин окна */
Wnormx= nx; Wnormy= ny; /* Координ. перпендикуляров */
/* Вычисление координат перпендикуляров к сторонам */
vox= *wx; voy= *wy;
ii= 0;
do {
if (++ii > kv) ii= 0;
vix= wx[ii]; viy= wy[ii]; /* Текущая вершина */
vnx= viy-voy; vny= vox-vix; /* Поворот по часовой */
if (splus) { /* Внутр нормали влево */
vnx= -vnx; vny= -vny;
}
*nx++= vnx; *ny++= vny;
vox= vix; voy= viy; /* Обновление координат */
} while (ii);
all:
return (otw);
} /* V_SetPclip */
/*------------------------------------------------- V_SetRclip
* Устанавливает прямоугольное окно отсечения
* Возвращает 0/1 - нет/есть ошибки в задании окна
*/
int V_SetRclip (xleft, ybottom, xright, ytop)
float xleft, ybottom, xright, ytop;
{ int otw;
otw= 0;
if (xleft >= xright || ybottom >= ytop) ++otw; else {
Windn= 4;
Windx= Wxrect; Windy= Wyrect; /* Вершины */
Wxlef= Wxrect[0]= Wxrect[1]= xleft;
Wybot= Wyrect[0]= Wyrect[3]= ybottom;
Wxrig= Wxrect[2]= Wxrect[3]= xright;
Wytop= Wyrect[1]= Wyrect[2]= ytop;
Wnormx= WxNrec; Wnormy= WyNrec; /* Нормали */
WxNrec[0]= 1; WyNrec[0]= 0;
WxNrec[1]= 0; WyNrec[1]= -1;
WxNrec[2]= -1; WyNrec[2]= 0;
WxNrec[3]= 0; WyNrec[3]= 1;
}
return (otw);
} /* V_SetRclip */
/*------------------------------------------------- V_GetRclip
* Возвращает текущее прямоугольное окно отсечения
*/
void V_GetRclip (xleft, ybottom, xright, ytop)
float *xleft, *ybottom, *xright, *ytop;
{
*xleft= Wxlef; *ybottom= Wybot;
*xright= Wxrig; *ytop= Wytop;
} /* V_GetRclip */
/*--------------------------------------------------- V_CSclip * Реализует алгоритм отсечения Коэна-Сазерленда с * кодированием концов отсекаемого отрезка * * int V_CSclip (float *x0, float *y0, float *x1, float *y1) * * Отсекает отрезок, заданный значениями координат его * точек (x0,y0), (x1,y1), по окну отсечения, заданному * глобальными скалярами Wxlef, Wybot, Wxrig, Wytop * * Конечным точкам отрезка приписываются коды, * характеризующие его положение относительно окна отсечения * по правилу: * * 1001 | 1000 | 1010 * -----|------|----- * | Окно | * 0001 | 0000 | 0010 * -----|------|----- * 0101 | 0100 | 0110 * * Отрезок целиком видим если оба его конца имеют коды 0000 * Если логическое И кодов концов не равно 0, то отрезок * целиком вне окна и он просто отбрасывается. * Если же результат этой операции = 0, то отрезок * подозрительный. Он может быть и вне и пересекать окно. * Для подозрительных отрезков определяются координаты их * пересечений с теми сторонами, с которыми они могли бы * пересечься в соответствии с кодами концов. * При этом используется горизонтальность и вертикальность * сторон окна, что позволяет определить одну из координат * без вычислений. * Часть отрезка, оставшаяся за окном отбрасывается. * Оставшаяся часть отрезка проверяется на возможность его * принятия или отбрасывания целиком. Если это невозможно, * то процесс повторяется для другой стороны окна. * На каждом цикле вычислений конечная точка отрезка, * выходившая за окно, заменяется на точку, лежащую или на * стороне окна или его продолжении. * * Вспомогательная процедура Code вычисляет код положения * для конца отрезка. * */
static float CSxn, CSyn; /* Координаты начала отрезка */
static int CScode (void) /* Определяет код точки xn, yn */
{ register int i;
i= 0;
if (CSxn < Wxlef) ++i; else
if (CSxn > Wxrig) i+= 2;
if (CSyn < Wybot) i+= 4; else
if (CSyn > Wytop) i+= 8;
return (i);
} /* CScode */
int V_CSclip (x0, y0, x1, y1)
float *x0, *y0, *x1, *y1;
{
float CSxk, CSyk; /* Координаты конца отрезка */
int cn, ck, /* Коды концов отрезка */
visible, /* 0/1 - не видим/видим*/
ii, s; /* Рабочие переменные */
float dx, dy, /* Приращения координат*/
dxdy,dydx, /* Наклоны отрезка к сторонам */
r; /* Рабочая переменная */
CSxk= *x1; CSyk= *y1;
CSxn= *x1; CSyn= *y1; ck= CScode ();
CSxn= *x0; CSyn= *y0; cn= CScode ();
/* Определение приращений координат и наклонов отрезка
* к осям. Заодно сразу на построение передается отрезок,
* состоящий из единственной точки, попавшей в окно
*/
dx= CSxk - CSxn;
dy= CSyk - CSyn;
if (dx != 0) dydx= dy / dx; else {
if (dy == 0) {
if (cn==0 && ck==0) goto out; else goto all;
}
}
if (dy != 0) dxdy= dx / dy;
/* Основной цикл отсечения */
visible= 0; ii= 4;
do {
if (cn & ck) break; /* Целиком вне окна */
if (cn == 0 && ck == 0) { /* Целиком внутри окна */
++visible; break;
}
if (!cn) { /* Если Pn внутри окна, то */
s= cn; cn= ck; ck= s; /* перестить точки Pn,Pk и */
r=CSxn; CSxn=CSxk; CSxk=r; /* их коды, чтобы Pn */
r=CSyn; CSyn=CSyk; CSyk=r; /* оказалась вне окна */
}
/* Теперь отрезок разделяется. Pn помещается в точку
* пересечения отрезка со стороной окна.
*/
if (cn & 1) { /* Пересечение с левой стороной */
CSyn= CSyn + dydx * (Wxlef-CSxn);
CSxn= Wxlef;
} else if (cn & 2) { /* Пересечение с правой стороной*/
CSyn= CSyn + dydx * (Wxrig-CSxn);
CSxn= Wxrig;
} else if (cn & 4) { /* Пересечение в нижней стороной*/
CSxn= CSxn + dxdy * (Wybot-CSyn);
CSyn= Wybot;
} else if (cn & 8) { /*Пересечение с верхней стороной*/
CSxn= CSxn + dxdy * (Wytop-CSyn);
CSyn= Wytop;
}
cn= CScode (); /* Перевычисление кода точки Pn */
} while (--ii >= 0);
if (visible) {
out: *x0= CSxn; *y0= CSyn;
*x1= CSxk; *y1= CSyk;
}
all:
return (visible);
} /* V_CSclip */
/*--------------------------------------------------- V_FCclip * Реализует алгоритм отсечения FC (Fast Clipping) * Собкова-Поспишила-Янга, с кодированием линий * * int V_FCclip (float *x0, float *y0, float *x1, float *y1) * * Отсекает отрезок, заданный значениями координат его * точек (x0,y0), (x1,y1), по окну отсечения, заданному * глобальными скалярами Wxlef, Wybot, Wxrig, Wytop * * Возвращает: * -1 - ошибка в задании окна * 0 - отрезок не видим * 1 - отрезок видим */
static float FC_xn, FC_yn, FC_xk, FC_yk;
static void Clip0_Top(void)
{FC_xn= FC_xn + (FC_xk-FC_xn)*(Wytop-FC_yn)/(FC_yk-FC_yn);
FC_yn= Wytop; }
static void Clip0_Bottom(void)
{FC_xn= FC_xn + (FC_xk-FC_xn)*(Wybot-FC_yn)/(FC_yk-FC_yn);
FC_yn= Wybot; }
static void Clip0_Right(void)
{FC_yn= FC_yn + (FC_yk-FC_yn)*(Wxrig-FC_xn)/(FC_xk-FC_xn);
FC_xn= Wxrig; }
static void Clip0_Left(void)
{FC_yn= FC_yn + (FC_yk-FC_yn)*(Wxlef-FC_xn)/(FC_xk-FC_xn);
FC_xn= Wxlef; }
static void Clip1_Top(void)
{FC_xk= FC_xk + (FC_xn-FC_xk)*(Wytop-FC_yk)/(FC_yn-FC_yk);
FC_yk= Wytop; }
static void Clip1_Bottom(void)
{FC_xk= FC_xk + (FC_xn-FC_xk)*(Wybot-FC_yk)/(FC_yn-FC_yk);
FC_yk= Wybot; }
static void Clip1_Right(void)
{FC_yk= FC_yk + (FC_yn-FC_yk)*(Wxrig-FC_xk)/(FC_xn-FC_xk);
FC_xk= Wxrig; }
static void Clip1_Left(void)
{FC_yk= FC_yk + (FC_yn-FC_yk)*(Wxlef-FC_xk)/(FC_xn-FC_xk);
FC_xk= Wxlef; }
int V_FCclip (x0, y0, x1, y1)
float *x0, *y0, *x1, *y1;
{ int Code= 0;
int visible= 0; /* Отрезок невидим */
FC_xn= *x0; FC_yn= *y0;
FC_xk= *x1; FC_yk= *y1;
/*
* Вычисление значения Code - кода отрезка
* Биты 0-3 - для конечной точки, 4-7 - для начальной
*
*/
if (FC_yk > Wytop) Code+= 8; else
if (FC_yk < Wybot) Code+= 4;
if (FC_xk > Wxrig) Code+= 2; else
if (FC_xk < Wxlef) Code+= 1;
if (FC_yn > Wytop) Code+= 128; else
if (FC_yn < Wybot) Code+= 64;
if (FC_xn > Wxrig) Code+= 32; else
if (FC_xn < Wxlef) Code+= 16;
/* Отсечение для каждого из 81-го случаев */
switch (Code) {
/* Из центра */
case 0x00: ++visible; break;
case 0x01: Clip1_Left() ; ++visible; break;
case 0x02: Clip1_Right(); ++visible; break;
case 0x04: Clip1_Bottom(); ++visible; break;
case 0x05: Clip1_Left() ;
if (FC_yk < Wybot) Clip1_Bottom();
++visible; break;
case 0x06: Clip1_Right();
if (FC_yk < Wybot) Clip1_Bottom();
++visible; break;
case 0x08: Clip1_Top(); ++visible; break;
case 0x09: Clip1_Left() ;
if (FC_yk > Wytop) Clip1_Top();
++visible; break;
case 0x0A: Clip1_Right();
if (FC_yk > Wytop) Clip1_Top();
++visible; break;
/* Слева */
case 0x10: Clip0_Left(); ++visible;
case 0x11: break; /* Отброшен */
case 0x12: Clip0_Left(); Clip1_Right();
++visible; break;
case 0x14: Clip0_Left();
if (FC_yn < Wybot) break; /* Отброшен */
Clip1_Bottom();
++visible;
case 0x15: break; /* Отброшен */
case 0x16: Clip0_Left();
if (FC_yn < Wybot) break; /* Отброшен */
Clip1_Bottom();
if (FC_xk > Wxrig) Clip1_Right();
++visible;
break;
case 0x18: Clip0_Left();
if (FC_yn > Wytop) break; /* Отброшен */
Clip1_Top();
++visible;
case 0x19: break; /* Отброшен */
case 0x1A: Clip0_Left();
if (FC_yn > Wytop) break; /* Отброшен */
Clip1_Top();
if (FC_xk > Wxrig) Clip1_Right();
++visible;
break;
/* Справа */
case 0x20: Clip0_Right(); ++visible; break;
case 0x21: Clip0_Right(); Clip1_Left(); ++visible;
case 0x22: break; /* Отброшен */
case 0x24: Clip0_Right();
if (FC_yn < Wybot) break; /* Отброшен */
Clip1_Bottom();
++visible;
break;
case 0x25: Clip0_Right();
if (FC_yn < Wybot) break; /* Отброшен */
Clip1_Bottom();
if (FC_xk < Wxlef) Clip1_Left();
++visible;
case 0x26: break; /* Отброшен */
case 0x28: Clip0_Right();
if (FC_yn > Wytop) break; /* Отброшен */
Clip1_Top();
++visible;
break;
case 0x29: Clip0_Right();
if (FC_yn > Wytop) break; /* Отброшен */
Clip1_Top();
if (FC_xk < Wxlef) Clip1_Left();
++visible;
case 0x2A: break; /* Отброшен */
/* Снизу */
case 0x40: Clip0_Bottom(); ++visible; break;
case 0x41: Clip0_Bottom();
if (FC_xn < Wxlef) break; /* Отброшен */
Clip1_Left() ;
if (FC_yk < Wybot) Clip1_Bottom();
++visible;
break;
case 0x42: Clip0_Bottom();
if (FC_xn > Wxrig) break; /* Отброшен */
Clip1_Right();
++visible;
case 0x44:
case 0x45:
case 0x46: break; /* Отброшен */
case 0x48: Clip0_Bottom();
Clip1_Top();
++visible;
break;
case 0x49: Clip0_Bottom();
if (FC_xn < Wxlef) break; /* Отброшен */
Clip1_Left() ;
if (FC_yk > Wytop) Clip1_Top();
++visible;
break;
case 0x4A: Clip0_Bottom();
if (FC_xn > Wxrig) break; /* Отброшен */
Clip1_Right();
if (FC_yk > Wytop) Clip1_Top();
++visible;
break;
/* Снизу слева */
case 0x50: Clip0_Left();
if (FC_yn < Wybot) Clip0_Bottom();
++visible;
case 0x51: break; /* Отброшен */
case 0x52: Clip1_Right();
if (FC_yk < Wybot) break; /* Отброшен */
Clip0_Bottom();
if (FC_xn < Wxlef) Clip0_Left();
++visible;
case 0x54:
case 0x55:
case 0x56: break; /* Отброшен */
case 0x58: Clip1_Top();
if (FC_xk < Wxlef) break; /* Отброшен */
Clip0_Bottom();
if (FC_xn < Wxlef) Clip0_Left();
++visible;
case 0x59: break; /* Отброшен */
case 0x5A: Clip0_Left();
if (FC_yn > Wytop) break; /* Отброшен */
Clip1_Right();
if (FC_yk < Wybot) break; /* Отброшен */
if (FC_yn < Wybot) Clip0_Bottom();
if (FC_yk > Wytop) Clip1_Top();
++visible;
break;
/* Снизу-справа */
case 0x60: Clip0_Right();
if (FC_yn < Wybot) Clip0_Bottom();
++visible;
break;
case 0x61: Clip1_Left() ;
if (FC_yk < Wybot) break; /* Отброшен */
Clip0_Bottom();
if (FC_xn > Wxrig) Clip0_Right();
++visible;
case 0x62:
case 0x64:
case 0x65:
case 0x66: break; /* Отброшен */
case 0x68: Clip1_Top();
if (FC_xk > Wxrig) break; /* Отброшен */
Clip0_Right();
if (FC_yn < Wybot) Clip0_Bottom();
++visible;
break;
case 0x69: Clip1_Left() ;
if (FC_yk < Wybot) break; /* Отброшен */
Clip0_Right();
if (FC_yn > Wytop) break; /* Отброшен */
if (FC_yk > Wytop) Clip1_Top();
if (FC_yn < Wybot) Clip0_Bottom();
++visible;
case 0x6A: break; /* Отброшен */
/* Сверху */
case 0x80: Clip0_Top();
++visible;
break;
case 0x81: Clip0_Top();
if (FC_xn < Wxlef) break; /* Отброшен */
Clip1_Left() ;
++visible;
break;
case 0x82: Clip0_Top();
if (FC_xn > Wxrig) break; /* Отброшен */
Clip1_Right();
++visible;
break;
case 0x84: Clip0_Top();
Clip1_Bottom();
++visible;
break;
case 0x85: Clip0_Top();
if (FC_xn < Wxlef) break; /* Отброшен */
Clip1_Left() ;
if (FC_yk < Wybot) Clip1_Bottom();
++visible;
break;
case 0x86: Clip0_Top();
if (FC_xn > Wxrig) break; /* Отброшен */
Clip1_Right();
if (FC_yk < Wybot) Clip1_Bottom();
++visible;
case 0x88:
case 0x89:
case 0x8A: break; /* Отброшен */
/* Сверху-слева */
case 0x90: Clip0_Left();
if (FC_yn > Wytop) Clip0_Top();
++visible;
case 0x91: break; /* Отброшен */
case 0x92: Clip1_Right();
if (FC_yk > Wytop) break; /* Отброшен */
Clip0_Top();
if (FC_xn < Wxlef) Clip0_Left();
++visible;
break;
case 0x94: Clip1_Bottom();
if (FC_xk < Wxlef) break; /* Отброшен */
Clip0_Left();
if (FC_yn > Wytop) Clip0_Top();
++visible;
case 0x95: break; /* Отброшен */
case 0x96: Clip0_Left();
if (FC_yn < Wybot) break; /* Отброшен */
Clip1_Right();
if (FC_yk > Wytop) break; /* Отброшен */
if (FC_yn > Wytop) Clip0_Top();
if (FC_yk < Wybot) Clip1_Bottom();
++visible;
case 0x98:
case 0x99:
case 0x9A: break; /* Отброшен */
/* Сверху-справа */
case 0xA0: Clip0_Right();
if (FC_yn > Wytop) Clip0_Top();
++visible;
break;
case 0xA1: Clip1_Left() ;
if (FC_yk > Wytop) break; /* Отброшен */
Clip0_Top();
if (FC_xn > Wxrig) Clip0_Right();
++visible;
case 0xA2: break; /* Отброшен */
case 0xA4: Clip1_Bottom();
if (FC_xk > Wxrig) break; /* Отброшен */
Clip0_Right();
if (FC_yn > Wytop) Clip0_Top();
++visible;
break;
case 0xA5: Clip1_Left() ;
if (FC_yk > Wytop) break; /* Отброшен */
Clip0_Right();
if (FC_yn < Wybot) break; /* Отброшен */
if (FC_yk < Wybot) Clip1_Bottom();
if (FC_yn > Wytop) Clip0_Top();
++visible;
case 0xA6: /* Отброшен */
case 0xA8:
case 0xA9:
case 0xAA: break;
/* Ошибка */
default: visible= -1;
break;
} /* switch */
if (visible > 0) {
*x0= FC_xn; *y0= FC_yn;
*x1= FC_xk; *y1= FC_yk;
}
return (visible);
} /* V_FCclip */
/*--------------------------------------------------- V_LBclip
* Реализует алгоритм отсечения Лианга-Барски
* с параметрическим заданием линий
*
* int V_LBclip (float *x0, float *y0, float *x1, float *y1)
*
* Отсекает отрезок, заданный значениями координат его
* точек (x0,y0), (x1,y1), по окну отсечения, заданному
* глобальными скалярами Wxlef, Wybot, Wxrig, Wytop
*
* Возвращает:
* 0 - отрезок не видим
* 1 - отрезок видим
*/
static float LB_t0, LB_t1;
static int LB_tclip (p, q)
float p, q;
{
int accept;
float r;
accept= 1; /* Отрезок принят */
if (p == 0) {
if (q < 0) accept= 0; /* Отбрасывание */
} else {
r= q/p;
if (p < 0) {
if (r > LB_t1) accept= 0; /* Отбрасывание */
else if (r > LB_t0) LB_t0= r;
} else {
if (r < LB_t0) accept= 0; /* Отбрасывание */
else if (r < LB_t1) LB_t1= r;
}
}
return (accept);
} /* LB_tclip */
int V_LBclip (x0, y0, x1, y1)
float *x0, *y0, *x1, *y1;
{ int visible;
float dx, dy;
visible= 0;
LB_t0= 0; LB_t1= 1;
dx= *x1 - *x0;
if (LB_tclip (-dx, *x0-Wxlef)) {
if (LB_tclip (dx, Wxrig-*x0)) {
dy= *y1 - *y0;
if (LB_tclip (-dy, *y0-Wybot)) {
if (LB_tclip (dy, Wytop-*y0)) {
if (LB_t1 < 1) {
*x1= *x0 + LB_t1*dx;
*y1= *y0 + LB_t1*dy;
}
if (LB_t0 > 0) {
*x0= *x0 + LB_t0*dx;
*y0= *y0 + LB_t0*dy;
}
++visible;
}
}
}
}
return (visible);
} /* V_LBclip */
/*--------------------------------------------------- V_CBclip * Реализует алгоритм отсечения Кируса-Бека * по произвольному выпуклому многоугольнику * с параметрическим заданием линий * * int V_CBclip (float *x0, float *y0, float *x1, float *y1) * * Отсекает отрезок, заданный значениями координат его * точек (x0,y0), (x1,y1), по окну отсечения, заданному * глобальными скалярами: * int Windn - количество вершин в окне отсечения * float *Windx, *Windy - массивы X,Y координат вершин * float *Wnormx, *Wnormy - массивы координат нормалей * к ребрам * * Возвращает: * 0 - отрезок не видим * 1 - отрезок видим */
int V_CBclip (x0, y0, x1, y1)
float *x0, *y0, *x1, *y1;
{ int ii, jj, visible, kw;
float xn, yn, dx, dy, r;
float CB_t0, CB_t1; /* Параметры концов отрезка */
float Qx, Qy; /* Положение относ ребра */
float Nx, Ny; /* Перпендикуляр к ребру */
float Pn, Qn; /**/
kw= Windn - 1; /* Ребер в окне */
visible= 1;
CB_t0= 0; CB_t1= 1;
dx= *x1 - (xn= *x0);
dy= *y1 - (yn= *y0);
for (ii=0; ii<=kw; ++ii) { /* Цикл по ребрам окна */
Qx= xn - Windx[ii]; /* Положения относ ребра */
Qy= yn - Windy[ii];
Nx= Wnormx[ii]; /* Перепендикуляр к ребру */
Ny= Wnormy[ii];
Pn= dx*Nx + dy*Ny; /* Скалярные произведения */
Qn= Qx*Nx + Qy*Ny;
/* Анализ расположения */
if (Pn == 0) { /* Паралл ребру или точка */
if (Qn < 0) {visible= 0; break; }
} else {
r= -Qn/Pn;
if (Pn < 0) { /* Поиск верхнего предела t */
if (r < CB_t0) {visible= 0; break; }
if (r < CB_t1) CB_t1= r;
} else { /* Поиск нижнего предела t */
if (r > CB_t1) {visible= 0; break; }
if (r > CB_t0) CB_t0= r;
}
}
}
if (visible) {
if (CB_t0 > CB_t1) visible= 0; else {
if (CB_t0 > 0) {
*x0= xn + CB_t0*dx;
*y0= yn + CB_t0*dy;
}
if (CB_t1 < 1) {
*x1= xn + CB_t1*dx;
*y1= yn + CB_t1*dy;
}
}
}
return (visible);
} /* V_CBclip */
/*=================================================== T_CLIP.C
*
* ТЕСТ ПРОЦЕДУР ОТСЕЧЕНИЯ
*/
#include <time.h>
#include <stdio.h>
/*--------------------------------------------------- V_DMclip
* Пустышка для процедур отсечения
*/
int V_DMclip (x0, y0, x1, y1)
float *x0, *y0, *x1, *y1;
{ int visible;
visible= 1;
return (visible);
} /* V_DMclip */
/*---------------------------------------------------- ClipMsg
* Печатает сообщение о результатах отсечения
*/
void ClipMsg (proc, visible, x0, y0, x1, y1, dt)
char *proc; int visible; float x0, y0, x1, y1, dt;
{
if (visible < 0) {
printf("*** ERROR (%s LineClip) - ", proc);
printf("ошибка в координатах окна. ");
printf("Прерывание с кодом ошибки 1.");
exit (1);
} else if (visible == 0)
printf ("%s: Line is no visible dt=%f\n", proc, dt);
else
printf ("%s: ClipLine: x0=%f y0=%f x1=%f y1=%f dt=%f\n",
proc, x0, y0, x1, y1, dt);
} /* ClipMsg */
/*---------------------------------------------- MAIN T_CLIP.C
*/
void main (void)
{
float Wxn, Wyn, Wxk, Wyk;
float Xn, Yn, Xk, Yk, x0, y0, x1, y1;
int ii, numb= 1;
float X_wind[100], Y_wind[100];
float X_norm[100], Y_norm[100];
int visible;
float dt;
time_t t1, t2;
long ll, powt=10l;
if (numb) goto set_win;
m0:printf ("----Вершин= %d ? ", numb);
scanf ("%d", &numb);
for (ii=0; ii<numb; ++ii) {
printf ("X_wind[%d], Y_wind[%d] ? ", ii, ii);
scanf ("%f%f", &X_wind[ii], &Y_wind[ii]);
}
ii= V_SetPclip (numb, X_wind, Y_wind, X_norm, Y_norm);
printf ("V_SetPclip= %d\n", ii);
if (ii) goto m0;
for (ii=0; ii<numb; ++ii)
printf ("ind=%d X_norm=%f, Y_norm=%f\n",
ii, X_norm[ii], Y_norm[ii]);
if (ii) goto m0;
/* Задание окна отсечения */
set_win:
powt= 1l;
V_GetRclip (&Wxn, &Wyn, &Wxk, &Wyk);
for (;;) {
printf ("Window: (Xn=%f Yn=%f Xk=%f Yk=%f) ? ",
Wxn, Wyn, Wxk, Wyk);
scanf ("%f%f%f%f", &Wxn, &Wyn, &Wxk, &Wyk);
if (!V_SetRclip (Wxn, Wyn, Wxk, Wyk)) break;
printf ("Error in a window boundarys\n");
}
/* Ввод координат отрезка */
Xn= Wxn-1.0; Yn= Wyn-1.0; Xk= Wxk+1.0; Yk= Wyk+1.0;
for (;;) {
printf ("------------- ");
printf ("ClipWindow: Xn=%f Yn=%f Xk=%f Yk=%f\n",
Wxlef, Wybot, Wxrig, Wytop);
printf ("New Line: (Xn=%f Yn=%f Xk=%f Yk=%f) ? ",
Xn, Yn, Xk, Yk);
scanf ("%f%f%f%f", &Xn, &Yn, &Xk, &Yk);
ll= powt;
t1= time(NULL);
do {
x0= Xn; y0= Yn; x1= Xk; y1= Yk;
visible= V_DMclip (&x0, &y0, &x1, &y1);
} while (--ll > 0l);
t2= time (NULL);
dt= ((float)(t2 - t1));
ClipMsg ("DM", visible, x0, y0, x1, y1, dt);
ll= powt;
t1= time(NULL);
do {
x0= Xn; y0= Yn; x1= Xk; y1= Yk;
visible= V_CSclip (&x0, &y0, &x1, &y1);
} while (--ll > 0l);
t2= time (NULL);
dt= ((float)(t2 - t1));
ClipMsg ("CS", visible, x0, y0, x1, y1, dt);
ll= powt;
t1= time(NULL);
do {
x0= Xn; y0= Yn; x1= Xk; y1= Yk;
visible= V_FCclip (&x0, &y0, &x1, &y1);
} while (--ll > 0l);
t2= time (NULL);
dt= ((float)(t2 - t1));
ClipMsg ("FC", visible, x0, y0, x1, y1, dt);
ll= powt;
t1= time(NULL);
do {
x0= Xn; y0= Yn; x1= Xk; y1= Yk;
visible= V_LBclip (&x0, &y0, &x1, &y1);
} while (--ll > 0l);
t2= time (NULL);
dt= ((float)(t2 - t1));
ClipMsg ("LB", visible, x0, y0, x1, y1, dt);
ll= powt;
t1= time(NULL);
do {
x0= Xn; y0= Yn; x1= Xk; y1= Yk;
visible= V_CBclip (&x0, &y0, &x1, &y1);
} while (--ll > 0l);
t2= time (NULL);
dt= ((float)(t2 - t1));
ClipMsg ("CB", visible, x0, y0, x1, y1, dt);
}
}
В данном приложении содержатся процедуры V_Plclip, реализующие простой алгоритм отсечения произвольного многоугольника по выпуклому многоугольному окну отсечения и тестовая программа проверки их работы.
Процедуры реализуют алгоритм, который, как и алгоритм Сазерленда-Ходгмана, последовательно отсекает весь многоугольник по каждому из ребер окна отсечения.
/*=================================================== V_PLCLIP
* Файл V_PLCLIP.C - процедуры простого алгоритма отсечния
* многоугольника
* Последняя редакция:
* 25.12.93 17:25
*/
#include <graphics.h>
#include "V_WINDOW.C" /* Глобалы и проц работы с окнами */
/* Включаемый файл V_WINDOW.C содержит
* подрограммы и глобалы для окон:
*
* V_SetPclip - установить размеры многоугольного окна
* отсечения
* V_GetPclip - опросить параметры многоугольного окна
* отсечения
* V_SetRclip - установить размеры прямоугольного окна
* отсечения
* V_GetRclip - опросить размеры прямоугольного окна
* отсечения
*
* Глобальные скаляры для алгоритмов отсечения по
* прямоугольному окну - Коэна-Сазерленда, Fc-алгоритм,
* Лианга-Барски
*
* static float Wxlef= 100.0, -- Координаты левого нижнего и
* Wybot= 100.0, -- правого верхнего углов окна
* Wxrig= 300.0, -- отсечения
* Wytop= 200.0;
*
* Глобальные скаляры для алгоритма Кируса-Бека
* отсечения по многоугольному окну
*
* Координаты прямоугольного окна
* static float Wxrect[4]= {100.0, 100.0, 300.0, 300.0 };
* static float Wyrect[4]= {100.0, 200.0, 200.0, 100.0 };
*
* Перепендикуляры к сторонам прямоугольного окна
* static float WxNrec[4]= {1.0, 0.0, -1.0, 0.0 };
* static float WyNrec[4]= {0.0, -1.0, 0.0, 1.0 };
*
* Данные для многоугольного окна
* static int Windn=4; -- Кол-во вершин у окна
* static float *Windx= Wxrect, -- Координаты вершин окна
* *Windy= Wyrect;
* static float *Wnormx= WxNrec, -- Координаты нормалей
* *Wnormy= WyNrec;
*/
/*-------------------------------------------------- Pl_clip0
* Служебная процедура, отсекает многоугольник
* относительно одного ребра окна
*
* Отсечение выполняется в цикле по сторонам многоугольника
* При первом входе в цикл только вычисляются величины для
* начальной точки: координаты, скалярное произведение,
* определяющее ее расположение относительно ребра окна, и
* код расположения.
* При последующих входах в цикл эти значения вычисляются
* для очередной вершины.
* По значениям кодов расположения вершин для стороны
* многоугольника определяется как она расположена
* относительно ребра и вычисляются координаты результирующего
* многоугольника.
*/
static int Pl_clip0 (N_reb, N_in, X_in, Y_in, X_ou, Y_ou)
int N_reb, N_in;
float *X_in, *Y_in, *X_ou, *Y_ou;
{
int ii, jj;
int pozb, /* Коды расположения начальной точки */
pozn, /* многоугольника и точек тек стороны */
pozk; /* 0/1/2 - пред точка вне/на/внутри */
float Rx,Ry; /* Координаты начала ребра окна */
float Nx, Ny; /* Нормаль к ребру окна */
float xb, yb; /* Начальная точка многоугольника */
float xn, yn; /* Начальная точка текущей стороны */
float xk, yk; /* Конечная точка текущей стороны */
float t; /* Значение параметра точки пересечения */
float Qb,Qn,Qk; /* Скалярные произведения */
float *ptx_ou;
/* Запрос параметров ребра окна */
Rx= Windx[N_reb]; Ry= Windy[N_reb];
Nx= Wnormx[N_reb]; Ny= Wnormy[N_reb];
/* Цикл отсчения многоугольника ребром окна */
ii= 0; ++N_in; ptx_ou= X_ou;
while (--N_in >= 0) {
if (N_in) {
xk= *X_in++; yk= *Y_in++; /* Кон точка стороны */
Qk= (xk-Rx)*Nx + (yk-Ry)*Ny; /* Параметр положения */
pozk= 1; /* 1 - точка на гр. */
if (Qk < 0) --pozk; else /* 0 - точка вне */
if (Qk > 0) ++pozk; /* 2 - точка внутри */
} else {
xk= xb; yk= yb; Qk= Qb; pozk= pozb;
}
if (!ii) {
xb= xn= xk; yb= yn= yk; Qb= Qn= Qk; pozb= pozn= pozk;
++ii; continue;
}
jj= 0;
switch (pozn*3 + pozk) { /* Стар Нов Выход */
case 0: goto no_point; /* вне-вне нет */
case 1: goto endpoint; /* вне-на конечная */
case 2: goto intersec; /* вне-вну перес,кон */
case 3: goto no_point; /* на -вне нет */
case 4: /* на -на конечная */
case 5: goto endpoint; /* на -вну конечная */
case 6: goto no_end; /* вну-вне пересечен */
case 7: /* вну-на конечная */
case 8: goto endpoint; /* вну-вну конечная */
}
no_end: ++jj;
intersec:
t= Qn/(Qn-Qk);
*X_ou++= xn + t*(xk-xn);
*Y_ou++= yn + t*(yk-yn);
if (!jj) {
endpoint:
*X_ou++= xk; *Y_ou++= yk;
}
no_point:
xn= xk; yn= yk; Qn= Qk; pozn= pozk;
}
return (X_ou - ptx_ou);
} /* Pl_clip0 */
/*--------------------------------------------------- V_Plclip
* Простая процедура отсечения многоугольника
* N_in - число вершин во входном многоугольнике
* X_in, Y_in - координаты вершин отсекаемого мног-ка
* этот массив будет испорчен
* Возвращает:
* < 0 - ошибки
* >= 0 - количество вершин в выходном многоугольнике
* X_ou, Y_ou - координаты вершин отсеченного многоугольника
*/
int V_Plclip (N_in, X_in, Y_in, X_ou, Y_ou)
int N_in;
float *X_in, *Y_in, *X_ou, *Y_ou;
{
int ii, N_ou; float *ptr;
if ((N_ou= N_in) < 3) {N_ou= -1; goto all; }
if (Windn < 3) {N_ou= -2; goto all; }
for (ii=0; ii<Windn; ++ii) {
N_ou= Pl_clip0 (ii, N_ou, X_in, Y_in, X_ou, Y_ou);
ptr= X_in; X_in= X_ou; X_ou= ptr;
ptr= Y_in; Y_in= Y_ou; Y_ou= ptr;
}
if (!(Windn & 1)) {
ii= N_ou;
while (--ii >= 0) {*X_ou++= *X_in++; *Y_ou++= *Y_in++; }
}
all:
return N_ou;
} /* V_Plclip */
/*=================================================== T_PLCLIP * ТЕСТ процедуры V_Plclip для отсечения многоугольника * * При первом входе устанавливается восьмиугольное окно * отсечения: * X: 150, 100, 100, 150, 250, 300, 300, 250 * Y: 100, 150, 250, 300, 300, 250, 150, 100 * * И на нем отсекается треугольник: * (10,160),(90,220),(170,160) * * Затем выдается запрос на количество вершин в * новом отсекаемом многоугольнике: * --- Vertexs in polyline= XX ? * При вводе числа > 0 будут запрашиваться координаты вершин * много-ка и выполняться его отсечение * При вводе числа = 0 программа затребует ввод координат * нового прямоугольного окна отсечения * При вводе числа < 0 программа запросит переустановку * многоугольного окна отсечения: * * ----Vertexs in clip window= XX ? * При вводе числа > 0 будут запрашиваться координаты вершин. * При вводе числа = 0 программа затребует ввод координат * прямоугольного окна. * При вводе числа < 0 программа закончится. */
#include <graphics.h>
#include "V_PLCLIP.C"
/*--------------------------------------------------- DrawPoly
* Чертит контур многоугольника
*/
void DrawPoly (col, n, x, y)
int col, n; float *x, *y;
{ int ii, jj;
setcolor (col);
for (ii=0; ii<n; ++ii) {
if ((jj= ii+1) >= n) jj= 0;
line (x[ii], y[ii], x[jj], y[jj]);
}
} /* DrawPoly */
/*---------------------------------------------------- CLR_STR
* Зачищает строку выводом в нее пробелов
*/
void CLR_STR (void)
{
printf (" \r");
}
/*------------------------------------------------ PLCLIP_MAIN
*/
void main (void)
{ int ii, jj,
fon; /* Индекс фона */
float Wxn,Wyn, /* Прямоугольный отсекатель */
Wxk,Wyk;
int N_wind= 0; /* Вводимый отсекатель */
float X_wind[100],
Y_wind[100];
float X_norm[100],
Y_norm[100];
int wnum; /* Запрошенный отсекатель */
float *wx,*wy,*wnx,*wny;
int N_poly= 0; /* Отсекаемый многугольник */
float X_poly[100],
Y_poly[100];
int N_clip= 0; /* Отсеченный многугольник */
float X_clip[100],
Y_clip[100];
int entry= 0; /* 0/1 - нет/был вывод по умолчанию */
int gdriver= DETECT, gmode;
initgraph (&gdriver, &gmode, "");
fon= 0; /* Цвет фона */
setbkcolor(fon); /* Очистка экрана */
cleardevice();
/*--------------- Установить окно отсечения ----------------*/
new_window:
gotoxy (1,1);
if (!entry) {
N_wind= 8; wx= X_wind; wy= Y_wind;
*wx++= 150; *wx++= 100; *wx++= 100; *wx++= 150;
*wy++= 100; *wy++= 150; *wy++= 250; *wy++= 300;
*wx++= 250; *wx++= 300; *wx++= 300; *wx++= 250;
*wy++= 300; *wy++= 250; *wy++= 150; *wy++= 100;
goto wr_window;
}
if (!N_poly) goto set_rect;
/*---------- Задание многоугольного окна отсечения ---------*/
set_window:
CLR_STR ();
printf ("----Vertexs in clip window= %d ? ", N_wind);
scanf ("%d", &N_wind);
if (N_wind < 0) goto all;
if (!N_wind) goto set_rect;
for (ii=0; ii<N_wind; ++ii) {
CLR_STR ();
printf ("X_wind[%d], Y_wind[%d] ? ", ii, ii);
scanf ("%f%f", &X_wind[ii], &Y_wind[ii]);
}
wr_window:
jj= V_SetPclip (N_wind, X_wind, Y_wind, X_norm, Y_norm);
if (jj) {
printf ("Error=%d in polyline window\n", jj);
goto set_window;
} else goto ou_win;
/*---------- Задание прямоугольного окна отсечения ---------*/
set_rect:
V_GetRclip (&Wxn, &Wyn, &Wxk, &Wyk);
get_rect:
CLR_STR ();
printf ("Rect window: (Xn=%f Yn=%f Xk=%f Yk=%f) ? ",
Wxn, Wyn, Wxk, Wyk);
scanf ("%f%f%f%f", &Wxn, &Wyn, &Wxk, &Wyk);
wr_rect:
jj= V_SetRclip (Wxn, Wyn, Wxk, Wyk);
if (jj) {
printf ("Error=%d in rectangle window\n", jj);
goto get_rect;
}
/*--------------- Прорисовка окна отсечения ----------------*/ ou_win: wnum= V_GetPclip (&wx, &wy, &wnx, &wny); DrawPoly (LIGHTRED, wnum, wx, wy);
/*------- Ввод координат отсекаемого многоугольника --------*/
set_poly:
gotoxy (1,1);
if (!entry) { /* При первом входе отрисовка по умолчанию */
N_poly= 3;
X_poly[0]= 10; X_poly[1]= 90; X_poly[2]= 170;
Y_poly[0]= 160; Y_poly[1]= 220; Y_poly[2]= 160;
} else {
CLR_STR ();
printf ("--- Vertexs in polyline= %d ? ",N_poly);
scanf ("%d", &N_poly);
if (N_poly <= 0) goto new_window;
for (ii=0; ii<N_poly; ++ii) {
printf (" \r");
printf ("X_poly[%d], Y_poly[%d] ? ", ii, ii);
scanf ("%f%f", &X_poly[ii], &Y_poly[ii]);
}
}
++entry;
/*---------- Прорисовка отсекателя и отсекаемого -----------*/
wnum= V_GetPclip (&wx, &wy, &wnx, &wny);
DrawPoly (LIGHTRED, wnum, wx, wy);
DrawPoly (LIGHTGREEN, N_poly, X_poly, Y_poly);
/*----------------------- Отсечение ------------------------*/
N_clip= V_Plclip(N_poly, X_poly, Y_poly, X_clip, Y_clip);
/*----------------- Прорисовка отсеченного -----------------*/
DrawPoly (YELLOW, N_clip, X_clip, Y_clip);
goto set_poly;
all:
closegraph();
} /* PLCLIP_MAIN */
1 Переход к модели с перечислением занятых точек также возможен из любой другой, но при решении проблем точности аппроксимации.